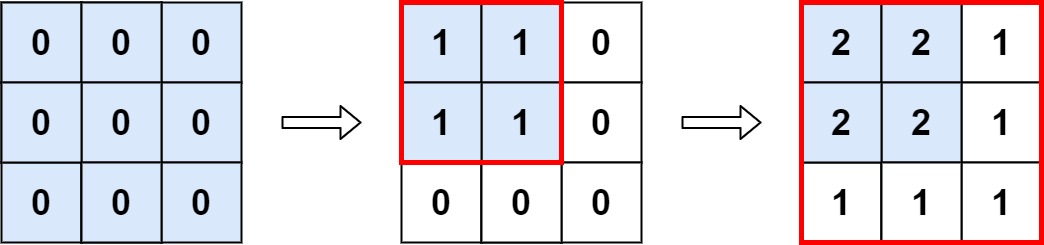
Problem: You are given an n x n binary matrix grid. You are allowed to change at most one 0 to be 1.
Return the size of the largest island in grid after applying this operation.
An island is a 4-directionally connected group of 1s.
Example:
Input: grid = [[1,0],[0,1]] Output: 3 Explanation: Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
Input: grid = [[1,1],[1,0]] Output: 4 Explanation: Change the 0 to 1 and make the island bigger, only one island with area = 4.
Input: grid = [[1,1],[1,1]] Output: 4 Explanation: Can't change any 0 to 1, only one island with area = 4.
Approach: If you see it is kind of (not exactly) connected components problem in Graph. We can solve it in 2 steps:
- We can first apply DFS from every cell which is not visited and has value 1. We will make this current cell parent for every reachable cell with value 1 using a map / 2D array. We also record the size of this component and we can store in a map with mapping like {parent_cell => component_size}.
- We again parse the grid and whenever we see a cell with 0. We can calculate it's neighbours component size and sum them. We add 1 into this sum as we are going to make this cell 1. This is what the island size we can get by changing this cell from 0 to 1. We can just take the maximum of all such islands' sizes and that will be our answer.
Implementation in C#:
public int LargestIsland(int[][] grid)
{
int rows = grid?.Length ?? 0;
if (rows == 0)
{
return 0;
}
int cols = grid[0].Length;
// To store component size
int[,] componentSizeMap = new int[rows, cols];
// To store component's parent
KeyValuePair<int?, int?>[,] componentParentMap = new KeyValuePair<int?, int?>[rows, cols];
for (int i = 0; i < rows; ++i)
{
for (int j = 0; j < cols; ++j)
{
KeyValuePair<int?, int?> currCell = new KeyValuePair<int?, int?>(i, j);
if (grid[i][j] == 1 &&
componentParentMap[i,j].Equals(default(KeyValuePair<int?, int?>)))
{
int componentSize = 0;
this.MakeComponentUsingDFS(
grid,
componentParentMap,
currCell,
i,
j,
ref componentSize);
componentSizeMap[i, j] = componentSize;
}
}
}
int maxSize = 0;
bool hasZero = false;
for (int i = 0; i < rows; ++i)
{
for (int j = 0; j < cols; ++j)
{
if (grid[i][j] == 0)
{
hasZero = true;
maxSize = Math.Max(
this.GetNeighborComponetSizesSum(
grid,
i,
j,
componentParentMap,
componentSizeMap) + 1,
maxSize);
}
}
}
return hasZero ? maxSize : rows * cols;
}
private int GetNeighborComponetSizesSum(
int[][] grid,
int row,
int col,
KeyValuePair<int?, int?>[,] componentParentMap,
int[,] componentSizeMap)
{
// Taking hashset as multiple neighbours can have same parent.
HashSet<KeyValuePair<int?, int?>> parentsSet = new HashSet<KeyValuePair<int?, int?>>();
//Left Neighbor
if (this.IsValidCell(grid, row - 1, col))
{
parentsSet.Add(componentParentMap[row - 1, col]);
}
//Right Neighbor
if (this.IsValidCell(grid, row + 1, col))
{
parentsSet.Add(componentParentMap[row + 1, col]);
}
//Top Neighbor
if (this.IsValidCell(grid, row, col - 1))
{
parentsSet.Add(componentParentMap[row, col - 1]);
}
//down Neighbor
if (this.IsValidCell(grid, row, col + 1))
{
parentsSet.Add(componentParentMap[row, col + 1]);
}
int neighborSize = 0;
foreach (var parent in parentsSet)
{
neighborSize += componentSizeMap[parent.Key.Value, parent.Value.Value];
}
return neighborSize;
}
private void MakeComponentUsingDFS(
int[][] grid,
KeyValuePair<int?, int?>[,] componentParentMap,
KeyValuePair<int?, int?> parent,
int currRow,
int currCol,
ref int componentSize)
{
if (!componentParentMap[currRow, currCol].Equals(default(KeyValuePair<int?, int?>)))
{
return;
}
componentParentMap[currRow, currCol] = parent;
++componentSize;
// Left Neighbor
if (this.IsValidCell(grid, currRow - 1, currCol))
{
this.MakeComponentUsingDFS(
grid,
componentParentMap,
parent,
currRow - 1,
currCol,
ref componentSize);
}
// Right Neighbor
if (this.IsValidCell(grid, currRow + 1, currCol))
{
this.MakeComponentUsingDFS(
grid,
componentParentMap,
parent,
currRow + 1,
currCol,
ref componentSize);
}
// Top Neighbor
if (this.IsValidCell(grid, currRow, currCol - 1))
{
this.MakeComponentUsingDFS(
grid,
componentParentMap,
parent,
currRow,
currCol - 1,
ref componentSize);
}
// Down Neighbor
if (this.IsValidCell(grid, currRow, currCol + 1))
{
this.MakeComponentUsingDFS(
grid,
componentParentMap,
parent,
currRow,
currCol + 1,
ref componentSize);
}
}
private bool IsValidCell(int[][] grid, int row, int col)
{
return row >= 0
&& row < grid.Length
&& col >= 0
&& col < grid[0].Length
&& grid[row][col] == 1;
}
Complexity: O(n^2)