[LeetCode]Range Addition II

Problem: You are given an m x n matrix M initialized with all 0's and an array of operations ops, where ops[i] = [ai, bi] means M[x][y] should be incremented by one for all 0 <= x < ai and 0 <= y < bi.

Count and return the number of maximum integers in the matrix after performing all the operations.

Example:

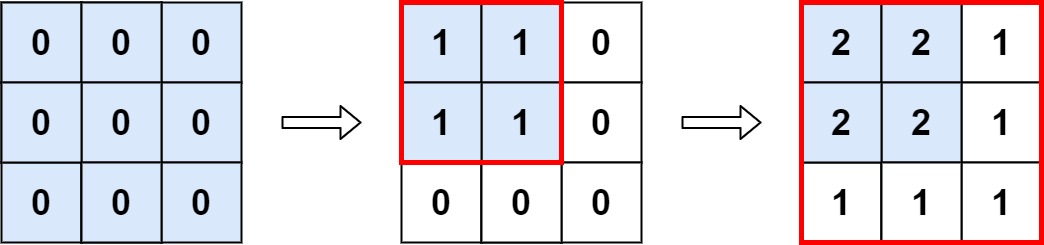
Input: m = 3, n = 3, ops = [[2,2],[3,3]]
Output: 4
Explanation: The maximum integer in M is 2, and there are four of it in M. So return 4.

Input: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
Output: 4

Input: m = 3, n = 3, ops = []
Output: 9

Approach: We can always opt the obvious brute force that is take a matrix of m x n and then apply all the operations. Once done we can parse the matrix and get the result but again it is expensive solution like any brute force solution. Let's try to optimize it.

Given in each operation, we are always incrementing matrix cells by one and this operation is applied from cell (0, 0] to (ai, bi), we can safely say the maximum number is always will be on the (0, 0) as in every operation value at cell (0, 0) is always going to be incremented. 

Now let's think about what will be the maximum number in the matrix?  Since we are increasing the values in the cells by 1, the maximum value in the matrix is always going to be the number of operations i.e. the length of ops. Now our final answer will be the number of cells having this value. How do we get it?

We just need to find the min of all ai's i.e. min of ops[i][0] where i = 0 to length of ops and bi's i.e. min of ops[i][1] where i = 0 to length of ops. Why min? What it is telling this row(min of ai's) x col(min of bi's) sub-matrix are always incremented by all the operations since all the operations are getting applied from  (0,0) to (ai, bi) so our answer will be row * col. 

Implementation in C#:

    public int MaxCount(int m, int n, int[][] ops) 

    {

        int maxNum = ops.Length;

        if (maxNum == 0)

        {

            return m * n;

        }

        int minRow = int.MaxValue, minCol = int.MaxValue;

        for (int i = 0; i < maxNum; ++i)

        {

            minRow = Math.Min(minRow, ops[i][0]);

            minCol = Math.Min(minCol, ops[i][1]);

        }    

        return minRow * minCol;

    }

Complexity: O(n) where n is the length of ops.