[LeetCode] Find the City With the Smallest Number of Neighbors at a Threshold Distance

Problem: There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between cities fromi and toi, and given the integer distanceThreshold.

Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.

Notice that the distance of a path connecting cities i and j is equal to the sum of the edges' weights along that path.

Example:

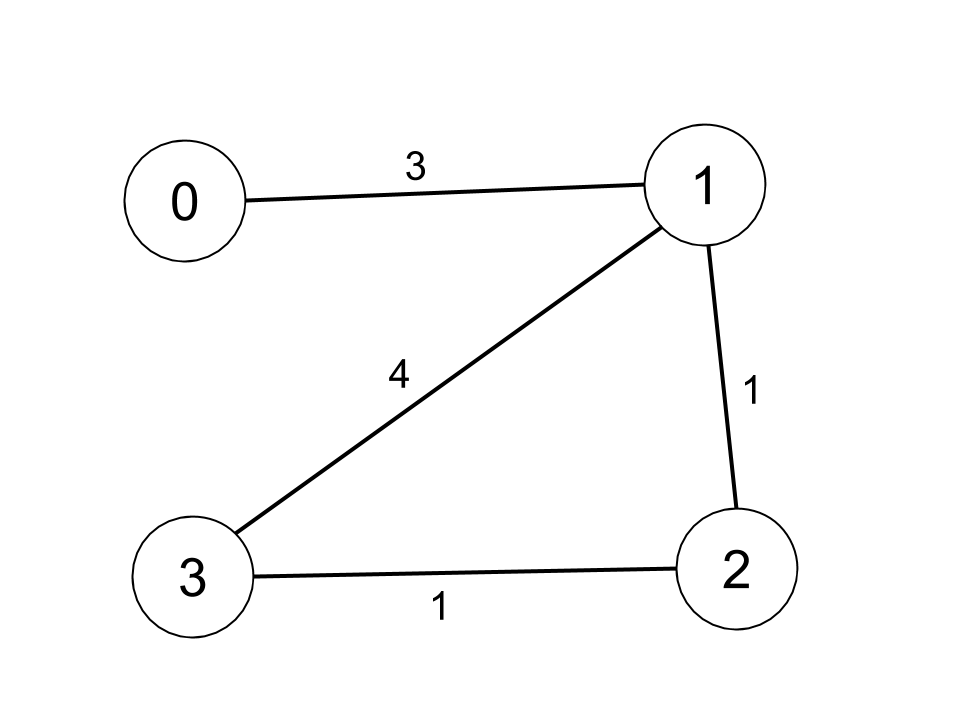
Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
Output: 3
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> [City 1, City 2] 
City 1 -> [City 0, City 2, City 3] 
City 2 -> [City 0, City 1, City 3] 
City 3 -> [City 1, City 2] 
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.

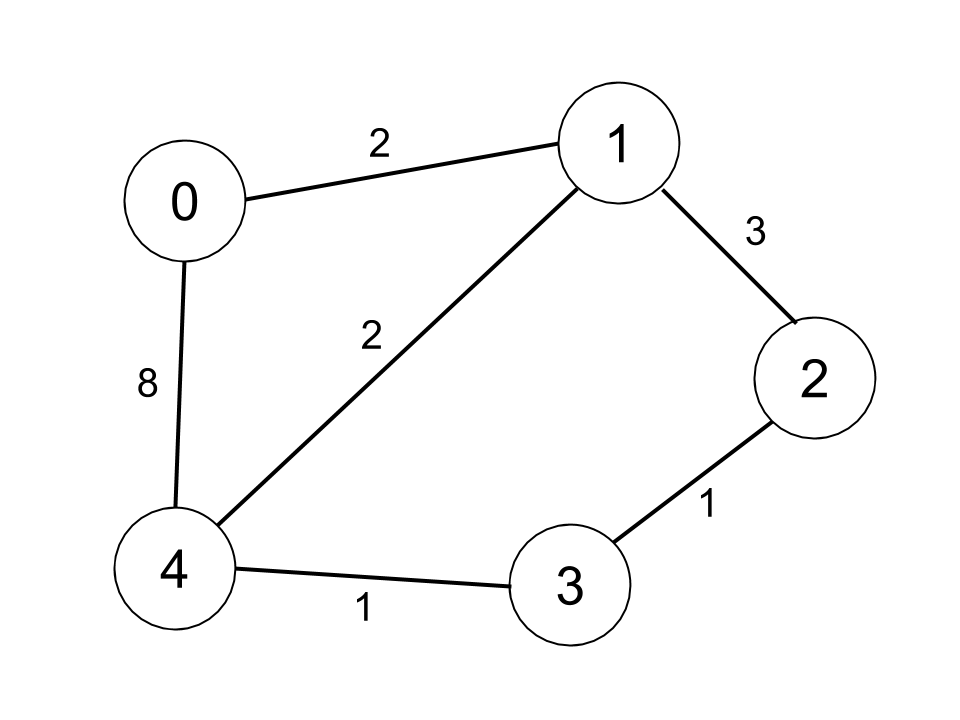
Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
Output: 0
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> [City 1] 
City 1 -> [City 0, City 4] 
City 2 -> [City 3, City 4] 
City 3 -> [City 2, City 4]
City 4 -> [City 1, City 2, City 3] 
The city 0 has 1 neighboring city at a distanceThreshold = 2.

Constraints:

• 2 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= fromi < toi < n
• 1 <= weighti, distanceThreshold <= 10^4
• All pairs (fromi, toi) are distinct.

Approach: This is clearly a Floyd-Warshall problem as we can do BFS here but the complexity will be n^n. Once we get the dist matrix from Floy Warshall algorithm, things becomes simpler. Now we know that we have the shortest path matrix 'dist' with us so we just need to traverse this matrix:

• For every node i from 0...n-1: 
• Check if dist[i][j] <= distanceThreshold then we know j is reachable from i.

Now in this way we just need to calculate the number of cities reachable from every city i and return the city with minimum number of connected cities.

Implementation in C#:

public class Solution

{

    public int FindTheCity(int n,

                           int[][] edges,

                           int distanceThreshold)

    {

        int[,] dist = this.FloydWarshall(edges, n);

        int minCount = INF;

        int minCity = -1;

        for (int i = 0; i < n; ++i)

        {

            int currCount = 0;

            for (int j = 0; j < n; ++j)

            {

                if (i != j)

                {

                    if (dist[i, j] <= distanceThreshold)

                    {

                        ++currCount;

                    }

                }

            }

            if (currCount <= minCount)

            {

                minCount = currCount;

                minCity = i;

            }

        }

        return minCity;

    }

    private int[,] FloydWarshall(int[][] edges, int n)

    {

        int[,] dist = this.InitDist(edges, n);

        for (int k = 0; k < n; ++k)

        {

            for (int i = 0; i < n; ++i)

            {

                for (int j = 0; j < n; ++j)

                {

                    if (dist[i, j] > dist[i, k] + dist[k, j])

                    {

                        dist[i, j] = dist[i, k] + dist[k, j];

                    }

                }

            }

        }

        return dist;

    }

    private int[,] InitDist(int[][] edges, int n)

    {

        int[,] dist = new int[n, n];

        for (int i = 0; i < n; ++i)

        {

            for (int j = 0; j < n; ++j)

            {

                dist[i, j] = i == j ? 0 : INF;

            }

        }

        foreach (var edge in edges)

        {

            dist[edge[0], edge[1]] = edge[2];

            dist[edge[1], edge[0]] = edge[2];

        }

        return dist;

    }

    // Max sum could be 10^4 * 10^2 = 10^6

    private const int INF = 9999999;

}

Complexity: O(n^3)

[LeetCode] Snakes and Ladders

Problem: You are given an n x n integer matrix board where the cells are labeled from 1 to n^2 in a Boustrophedon style starting from the bottom left of the board (i.e. board[n - 1][0]) and alternating direction each row.

You start on square 1 of the board. In each move, starting from square curr, do the following:

• Choose a destination square next with a label in the range [curr + 1, min(curr + 6, n^2)].
• This choice simulates the result of a standard 6-sided die roll: i.e., there are always at most 6 destinations, regardless of the size of the board.
• If next has a snake or ladder, you must move to the destination of that snake or ladder. Otherwise, you move to next.
• The game ends when you reach the square n^2.

A board square on row r and column c has a snake or ladder if board[r][c] != -1. The destination of that snake or ladder is board[r][c]. Squares 1 and n2 do not have a snake or ladder.

Note that you only take a snake or ladder at most once per move. If the destination to a snake or ladder is the start of another snake or ladder, you do not follow the subsequent snake or ladder.

• For example, suppose the board is [[-1,4],[-1,3]], and on the first move, your destination square is 2. You follow the ladder to square 3, but do not follow the subsequent ladder to 4.

Return the least number of moves required to reach the square n2. If it is not possible to reach the square, return -1.

Example:

Input: board = [[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]]
Output: 4
Explanation: 
In the beginning, you start at square 1 (at row 5, column 0).
You decide to move to square 2 and must take the ladder to square 15.
You then decide to move to square 17 and must take the snake to square 13.
You then decide to move to square 14 and must take the ladder to square 35.
You then decide to move to square 36, ending the game.
This is the lowest possible number of moves to reach the last square, so return 4.

Approach: This is again a BFS problem. You can assume the snake and ladder board as a graph in which one cell is connected to another cell using snake or ladder. Now we need to find the path with minimum nodes from 1 to n*n, which is clearly a BFS problem.

Now the only thing we need is given the number next , we need to calculate it's cell (row, col).

Implementation in C#:

    public int SnakesAndLadders(int[][] board)

    {

        int n = board?.Length ?? 0;

        if (n == 0)

        {

            return 0;

        }

        int numOfSteps = 0;

        Queue<int> queue = new Queue<int>();

        queue.Enqueue(1);

        HashSet<int> visited = new HashSet<int>();

        while (queue.Count > 0)

        {

            ++numOfSteps;

            int size = queue.Count;

            for (int i = 0; i < size; ++i)

            {

                int curr = queue.Dequeue();

                for (int j = 1; j <= 6; ++j)

                {

                    int next = curr + j;

                    // Reached target

                    if (next == n * n)

                    {

                        return numOfSteps;

                    }

                    int row = 0;

                    int col = 0;

                    // Get cell of the given number next

                    this.GetNextRowColumn(next, n, ref row, ref col);

                    // if curr cell is snake or stair

                    if (board[row][col] != -1)

                    {

                        next = board[row][col];

                    }

                    // Reached target

                    if (next == n * n)

                    {

                        return numOfSteps;

                    }

                    if (!visited.Contains(next))

                    {

                        visited.Add(next);

                        queue.Enqueue(next);

                    }

                }

            }

        }

        return -1;

    }

    private void GetNextRowColumn(int next, int n, ref int row, ref int col)

    {

        row = next / n;

        col = next % n;

        if (col == 0)

        {

            col = n;

            --row;

        }

        col = row % 2 == 0 ? col - 1 : n - col;

        row = n - 1 - row;

    }

Complexity: O(n^2)

[LeetCode] Nearest Exit from Entrance in Maze

Problem: You are given an m x n matrix maze (0-indexed) with empty cells (represented as '.') and walls (represented as '+'). You are also given the entrance of the maze, where entrance = [entrancerow, entrancecol] denotes the row and column of the cell you are initially standing at.

In one step, you can move one cell up, down, left, or right. You cannot step into a cell with a wall, and you cannot step outside the maze. Your goal is to find the nearest exit from the entrance. An exit is defined as an empty cell that is at the border of the maze. The entrance does not count as an exit.

Return the number of steps in the shortest path from the entrance to the nearest exit, or -1 if no such path exists.

Example:

Input: maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
Output: 1
Explanation: There are 3 exits in this maze at [1,0], [0,2], and [2,3].
Initially, you are at the entrance cell [1,2].
- You can reach [1,0] by moving 2 steps left.
- You can reach [0,2] by moving 1 step up.
It is impossible to reach [2,3] from the entrance.
Thus, the nearest exit is [0,2], which is 1 step away.

Input: maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
Output: 2
Explanation: There is 1 exit in this maze at [1,2].
[1,0] does not count as an exit since it is the entrance cell.
Initially, you are at the entrance cell [1,0].
- You can reach [1,2] by moving 2 steps right.
Thus, the nearest exit is [1,2], which is 2 steps away.

Input: maze = [[".","+"]], entrance = [0,0]
Output: -1
Explanation: There are no exits in this maze.

Approach: This is clearly a Graph BFS problem where a cell is connected to another cell if the other cell is one of top, bottom, left or right cell of the current cell. We just need to find the shortest path from the given cell 'entrance' to any empty cell (contains '.') on the boundary. To get this path we can use BFS as there is same weight here on every edge.

That's all!

Implementation in C#:

    public int NearestExit(char[][] maze, int[] entrance)

    {

        int rows = maze?.Length ?? 0;

        if (rows == 0)

        {

            return -1;

        }

        int cols = maze[0].Length;

        var queue = new Queue<int[]>();

        maze[entrance[0]][entrance[1]] = '+';

        this.AddValidNeighboursToQueue(maze, queue, entrance[0], entrance[1]);

        int steps = 1;

        while (queue.Count > 0)

        {

            int size = queue.Count;

            for (int i = 0; i < size; ++i)

            {

                var cell = queue.Dequeue();

                if (this.IsBoundaryCell(cell, rows, cols))

                {

                    return steps;

                }

                this.AddValidNeighboursToQueue(maze, queue, cell[0], cell[1]);

            }

            ++steps;

        }

        return -1;

    }

    private bool IsBoundaryCell(int[] cell, int rows, int cols)

    {

        return cell[0] == 0 ||

               cell[0] == rows - 1 ||

               cell[1] == 0 ||

               cell[1] == cols - 1;

    }

    private void AddValidNeighboursToQueue(char[][] maze,

                                           Queue<int[]> queue,

                                           int row,

                                           int col)

    {

        // Left neighbour

        if (this.IsValidAndEmptyCell(maze, row, col - 1))

        {

            maze[row][col - 1] = '+';

            queue.Enqueue(new int[] {row, col - 1});

        }

        // Right neighbour

        if (this.IsValidAndEmptyCell(maze, row, col + 1))

        {

            maze[row][col + 1] = '+';

            queue.Enqueue(new int[] {row, col + 1});

        }

        // Top neighbour

        if (this.IsValidAndEmptyCell(maze, row - 1, col))

        {

            maze[row - 1][col] = '+';

            queue.Enqueue(new int[] {row - 1, col});

        }

        // Bottom neighbour

        if (this.IsValidAndEmptyCell(maze, row + 1, col))

        {

            maze[row + 1][col] = '+';

            queue.Enqueue(new int[] {row + 1, col});

        }

    }

    private bool IsValidAndEmptyCell(char[][] maze, int row, int col)

    {

        return row >= 0 &&

               row < maze.Length &&

               col >= 0 &&

               col < maze[0].Length &&

               maze[row][col] == '.';

    }

Complexity: O(n)

[LeetCode] Reorder Routes to Make All Paths Lead to the City Zero

Problem: There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.

Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi.

This year, there will be a big event in the capital (city 0), and many people want to travel to this city.

Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.

It's guaranteed that each city can reach city 0 after reorder.

Example:

Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
Output: 2
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Constraints:

• 2 <= n <= 5 * 104
• connections.length == n - 1
• connections[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi

Approach: This is clearly a graph as it is already mentioned in the question. Now the intuition is simple all the outgoing edges from 0 must be reversed so that there is a path to reach 0 from every city because it is given that there is only one path between two cities.

Now once the edges from 0 is reversed. We need to do the same for cities directly connected to 0 as there must be incoming path to every city x which is directly connected to 0 from every city directly connected to x, Right? See from example:

0 -> x -> y. We have reversed the path from 0 to x so now graph looks like 0 <- x -> y. How somebody will reach from city y to 0? We need to reverse the path x -> y so that the way now is 0 <- x <- y.

We will keep doing it recursively. With this intuition we can solve this problem using DFS but there are still some problems. Let's see it by example -

0 <- x -> y. As per our graph, there is no outgoing edge from 0 to x so we won't do anything and will return count as 0 as there is no neighbour of 0 given it's directed graph but we can see we have to reverse x -> y path. That means we must have incoming edges too in our graph.

Now the problem is if we store incoming edges how we will come to know if it is incoming edge and I should not reverse it? We can store the original edges in a set and compare before incresasing the count of edges to reverse but what I am doing it in my implementation is that I am pushing negative of city value to identify it given the cities are in range from 0 to n - 1.

Another problem is in case of outgoing edge to node's parent.We should not increase the count in case the connected city or neighbour city is it's parent, right. Consider this example:

0 -> 1 <- 2

Here we will have an positive edge from 2 -> 1 and as per our logice we will increase the count but it should not be the case. To avoid it we just need to check if the edge is ougoing to it's parent itself. Please note that this is happening because we are pushing incoming edges too in our graph.  

Hopefully it's clear now. 

Implementation in C#:

    public int MinReorder(int n, int[][] connections)

    {

        if (n <= 1)

        {

            return 0;

        }

        var cityGraph = this.GenerateCityGraph(connections);

        HashSet<int> visited = new HashSet<int>();

        return this.MinReorderDFS(cityGraph, 0, -1, visited);

    }

    private int MinReorderDFS(Dictionary<int, List<int>> cityGraph,

                              int currCity,

                              int parentCity,

                              HashSet<int> visited)

    {

        if (visited.Contains(currCity))

        {

            return 0;

        }

        visited.Add(currCity);

        int count = 0;

        if (cityGraph.ContainsKey(currCity))

        {

            foreach (int city in cityGraph[currCity])

            {

                if (city > 0 && city != parentCity)

                {

                    ++count;

                }

                count += this.MinReorderDFS(cityGraph,

                                            Math.Abs(city),

                                            currCity,

                                            visited);

            }

        }

        return count;

    }

    private Dictionary<int, List<int>> GenerateCityGraph(int[][] connections)

    {

        var cityGraph = new Dictionary<int, List<int>>();

        foreach (var connection in connections)

        {

            if (!cityGraph.ContainsKey(connection[0]))

            {

                cityGraph[connection[0]] = new List<int>();

            }

            cityGraph[connection[0]].Add(connection[1]);

            if (!cityGraph.ContainsKey(connection[1]))

            {

                cityGraph[connection[1]] = new List<int>();

            }

            cityGraph[connection[1]].Add(-connection[0]);

        }

        return cityGraph;

    }

Complexity: O(n)

[LeetCode] Number of Provinces

Problem: There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.

A province is a group of directly or indirectly connected cities and no other cities outside of the group.

You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.

Return the total number of provinces.

Example:

Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2

Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3

Approach: Its kind of finding connected components in a graph problem. We will simply count the number of times we need to do a DFS until all the nodes are visited.

Implementation in C#:

    public int FindCircleNum(int[][] isConnected)

    {

        int rows = isConnected?.Length ?? 0;

        if (rows == 0)

        {

            return 0;

        }

        int cols = isConnected[0].Length;

        HashSet<int> visited = new HashSet<int>();

        int numOfProvinces = 0;

        for (int node = 0; node < rows; ++node)

        {

            if (!visited.Contains(node))

            {

                this.FindCircleNumDFS(node, isConnected, visited);

                ++numOfProvinces;

            }

        }

        return numOfProvinces;

    }

    private void FindCircleNumDFS(int node,

                                  int[][] isConnected,

                                  HashSet<int> visited)

    {

        if (visited.Contains(node))

        {

            return;

        }

        visited.Add(node);

        for (int i = 0; i < isConnected[0].Length; ++i)

        {

            if (isConnected[node][i] == 1)

            {

                this.FindCircleNumDFS(i, isConnected, visited);

            }

        }

    }

Complexity: O(n^2)

[Google][LeetCode] Keys and Rooms

Problem: There are n rooms labeled from 0 to n - 1 and all the rooms are locked except for room 0. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.

When you visit a room, you may find a set of distinct keys in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.

Given an array rooms where rooms[i] is the set of keys that you can obtain if you visited room i, return true if you can visit all the rooms, or false otherwise.

Example:

Input: rooms = [[1],[2],[3],[]]
Output: true
Explanation: 
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.

Input: rooms = [[1,3],[3,0,1],[2],[0]]
Output: false
Explanation: We can not enter room number 2 since the only key that unlocks it is in that room.

Approach: If we look at this problem closely, we will come to know the given array is kind of a graph where one node is connected to another node (room) if it has key to that room so we just need to DFS on this graph and check if the number of visited nodes are equal to the number of rooms. If yes, return true; false otherwise.

Implementation in C#:

    public bool CanVisitAllRooms(IList<IList<int>> rooms)

    {

        int numOfRooms = rooms?.Count ?? 0;

        if (numOfRooms <= 1)

        {

            return true;

        }

        HashSet<int> visitedRooms = new HashSet<int>();

        this.CanVisitAllRoomsDFS(rooms, 0, visitedRooms);

        return visitedRooms.Count == numOfRooms;

    }

    private void CanVisitAllRoomsDFS(IList<IList<int>> rooms,

                                     int currRoom,

                                     HashSet<int> visitedRooms)

    {

        if (visitedRooms.Contains(currRoom))

        {

            return;

        }

        visitedRooms.Add(currRoom);

        IList<int> neighbourRooms = rooms[currRoom];

        foreach (int room in neighbourRooms)

        {

            this.CanVisitAllRoomsDFS(rooms, room, visitedRooms);

        }

    }

Complexity: O(n)