Delete Node in a BST

Problem: Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

1. Search for a node to remove.
2. If the node is found, delete the node.

Example:

Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.

Approach: Approach is going to be same as mentioned in the question itself. First we find the node using the approach in search in binary search tree. 

Now the removal part is lil tricky. Here are the steps we can take:

• If the node to remove is leaf node, we simply remove it.
• If the node has just one child then we can just assign node to it's child.
• Now the most tricky situation where both the children are not null, here we can take one of the following two appoaches:

1. Take the right most child of node's left subtree. Assign it's value to node's value. Now call this method recursively to remove this value from node's left subtree.
2. Take the left most child of node's right subtree. Assign it's value to node's value. Now call this method recursively to remove this value from node's right subtree.

That's all!

Implemenation in C#:

    public TreeNode DeleteNode(TreeNode root, int key)

    {

        if (root == null)

        {

            return root;

        }

        if (root.val == key)

        {

            if (root.right != null && root.left != null)

            {

                root.val = this.FindLeftMostNodeValue(root.right);

                root.right = this.DeleteNode(root.right, root.val);

            }

            else

            {

                if (root.left != null)

                {

                    return root.left;

                }

                else

                {

                    return root.right;

                }

            }

        }

        if (root.val < key)

        {

            root.right = this.DeleteNode(root.right, key);

        }

        else

        {

            root.left = this.DeleteNode(root.left, key);

        }      

        return root;

    }

    private int FindLeftMostNodeValue(TreeNode node)

    {

        while(node.left != null)

        {

            node = node.left;

        }

        return node.val;

    }

Complexity: O(n)

Search in a Binary Search Tree

Problem: You are given the root of a binary search tree (BST) and an integer val.

Find the node in the BST that the node's value equals val and return the subtree rooted with that node. If such a node does not exist, return null.

Example:

Input: root = [4,2,7,1,3], val = 2
Output: [2,1,3]

Input: root = [4,2,7,1,3], val = 5
Output: []

Approach: It's a simple problem to solve where we can use pre order traversal. We can take advantage of this tree being  binary search tree. At every node, we take following steps:

• If node.value is equal to val, return node.
• If node.value is less than val , search on node's righ subtree.
• Else search on node's left subtree.
• If node is null return null.

That's all!

Implementation in C#:

    public TreeNode SearchBST(TreeNode root, int val)

    {

        if (root == null)

        {

            return null;

        }

        if (root.val == val)

        {

            return root;

        }

        return root.val < val ?

               this.SearchBST(root.right, val) :

               this.SearchBST(root.left, val);

    }

Complexity: Average: O(logn), Worst: O(n) where tree is linked list.

[LeetCode] Minimum Absolute Difference in BST

Problem: Given the root of a Binary Search Tree (BST), return the minimum absolute difference between the values of any two different nodes in the tree.

Example:

Input: root = [4,2,6,1,3]
Output: 1

Input: root = [1,0,48,null,null,12,49]
Output: 1

Approach: A simple inorder traversal is enough to solve this problem as this tree is BST and inorder traversal will output the values in sorted order. Directly look at the implementation to understand the approach better.

Implementation in C#:

    public int GetMinimumDifference(TreeNode root) 

    {

        if (root == null)

        {

            return 0;

        }

        TreeNode prev = null;

        int minDiff = int.MaxValue;

        this.GetMinDiff(root, ref prev, ref minDiff);

        return minDiff;

    }

    

    private void GetMinDiff(TreeNode node, ref TreeNode prev, ref int minDiff)

    {

        if (node == null)

        {

            return;

        }    

        this.GetMinDiff(node.left, ref prev, ref minDiff);

        if (prev != null)

        {

            minDiff = Math.Min(minDiff, Math.Abs(node.val - prev.val));

        }

        prev = node;

        this.GetMinDiff(node.right, ref prev, ref minDiff);

    }

Complexity: O(n)

[LeetCode] Find Mode in Binary Search Tree

Problem: Given the root of a binary search tree (BST) with duplicates, return all the mode(s) (i.e., the most frequently occurred element) in it.

If the tree has more than one mode, return them in any order.

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than or equal to the node's key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
• Both the left and right subtrees must also be binary search trees.

Example:

Input: root = [1,null,2,2]
Output: [2]

Approach: A simple inorder traversal can work here as in case of BST, inorder traversal will give the output in sorted order. Just look at the implementation to understand it.

Implementation in C#:

    public int[] FindMode(TreeNode root) 

    {

        if (root == null)

        {

            return null;

        }      

        int max = 0;

        TreeNode prevNode = null;

        int prevFreq = 0;

        List<int> result = new List<int>();   

        this.FindModeInorder(root, ref prevNode, ref prevFreq, result, ref max);

        return result.ToArray();

    }

    

    private void FindModeInorder(TreeNode node,

                                ref TreeNode prevNode,

                                ref int prevFreq,

                                List<int> result,

                                ref int max)

    {

        if (node == null)

        {

            return;

        }

        this.FindModeInorder(node.left, ref prevNode, ref prevFreq, result, ref max);

        if (prevNode != null)

        {

            if (node.val == prevNode.val)

            {

                ++prevFreq;

            }

            else

            {

                prevFreq = 1;

            }

        }

        else

        {

            // Current node is the leftmost node

            ++prevFreq;

            max = prevFreq;

        }

        prevNode = node;

        if (prevFreq > max)

        {

            max = prevFreq;

            result.Clear();

            result.Add(node.val);

        }

        else if(prevFreq == max)

        {

            result.Add(node.val);

        }

        this.FindModeInorder(node.right, ref prevNode, ref prevFreq, result, ref max);

    }

Complexity: O(n)

[LeetCode] Serialize and Deserialize BST

Problem: Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary search tree. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.

The encoded string should be as compact as possible.

Example:

Input: root = [2,1,3]
Output: [2,1,3]

Input: root = []
Output: []

Approach: We will store the preorder traversal here as inorder traversal is already known which is sorted order.

Implementation in C#:

    public string serialize(TreeNode root) 

    {

        if(root == null)

        {

            return string.Empty;

        }

        return string.Join('|', this.PreOrderSerialize(root));

    }

    public TreeNode deserialize(string data) 

    {

        if (string.IsNullOrWhiteSpace(data))

        {

            return null;

        }        

        List<string> nodeValues = data.Split("|").ToList();

        TreeNode root = new TreeNode(int.Parse(nodeValues[0]));

        this.MakeTree(nodeValues, root);        

        return root;

    }

    

    private void MakeTree(List<string> nodeValues, TreeNode root)

    {

        Stack<TreeNode> stackOfTreeVals = new Stack<TreeNode>();

        stackOfTreeVals.Push(root);

        for (int i = 1; i < nodeValues.Count; ++i)

        {

            TreeNode node = stackOfTreeVals.Peek();

            int currVal = int.Parse(nodeValues[i]);

            if (currVal < node.val)

            {

                node.left = new TreeNode(currVal);

                stackOfTreeVals.Push(node.left);

            }

            else

            {

                while(stackOfTreeVals.Count > 0 && stackOfTreeVals.Peek().val < currVal)

                {

                    node = stackOfTreeVals.Peek();

                    stackOfTreeVals.Pop();

                }

                node.right = new TreeNode(currVal);

                stackOfTreeVals.Push(node.right);

            }

        }

    }

    

    private List<string> PreOrderSerialize(TreeNode node) 

    {

        List<string> result = new List<string>();

        if (node == null)

        {

            return result;

        }

        result.Add(node.val.ToString());

        result.AddRange(this.PreOrderSerialize(node.left));

        result.AddRange(this.PreOrderSerialize(node.right));

        return result;

    }

Complexity: O(n)

[LeetCode] Two Sum IV - Input is a BST

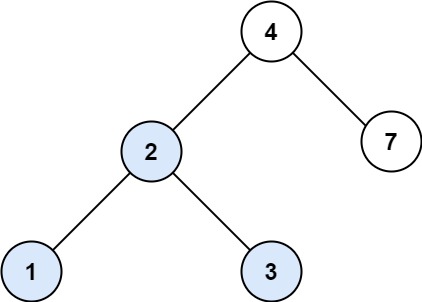
Problem: Given the root of a Binary Search Tree and a target number k, return true if there exist two elements in the BST such that their sum is equal to the given target.

Example:

Input: root = [5,3,6,2,4,null,7], k = 9
Output: true

Input: root = [5,3,6,2,4,null,7], k = 28
Output: false

Input: root = [2,1,3], k = 4
Output: true

Input: root = [2,1,3], k = 1
Output: false

Input: root = [2,1,3], k = 3
Output: true

Approach: There are multiple approaches we can take here to solve this problem. One of simplest approach would be to take one node of binary search tree and then search for k - node.val in the input binary search tree. Here is how the approach looks like:

• DEF DoesSumExist(root, node, k):
• IF node == NULL
• RETURN FALSE
• IF (DoesElementExist(root , k - node.val))
• RETURN TRUE
• RETURN DoesSumExist(root, node.left, k) OR DoesSumExist(root, node.right, k)

• DEF DoesElementExist(node, val):
• WHILE node ! = null
• IF node.val == val
• RETURN TRUE
• ELSE IF node.val < val
• node = node.right
• ELSE
• node = node.left
• RETURN FALSE

The above approach will work but this approach will take O(nlogn) time. Let's try to optimize it. What we can do is we can store this BSTree in an array using inorder traversal. This will make sure the array is sorted. Now we can use two pointer approach to find the two elements whose sum is equal to k. Here is the algorithm:

• DEF DoesSumExist(root, k)
• sortedArray = []
• PutElementsInSortedArray(root, sortedArray)
• RETURN DoesSumExistInSortedArray(sortedArray, k)

• DEF PutElementsInSortedArray(node, sortedArray)
• IF node != null
• PutElementsInSortedArray(node.left, sortedArray)
• sortedArray.Add(node.val)
• PutElementsInSortedArray(node.right, sortedArray)

• DEF DoesSumExistInSortedArray(sortedArray, k)
• start = 0, end = Length(sortedArray) - 1
• WHILE start < end
• sum = sortedArray[start] + sortedArray[end]
• IF sum == k
• RETURN TRUE
• ELSE sum < k
• start = start + 1
• ELSE
• end = end - 1
• RETURN FALSE

The above approach will solve the problem in linear time which is definitely a considerable improvement but if you see we are traversing the same elements twice (once in tree and once in array) and also we are taking O(n) space every time. Let's try to do better!

We can use hashing here to solve this problem efficiently. We can use any traversal and we keep putting the values(node.val) in the hash set. Now at any time if we find k - node.val in hash set we can return true immediately otherwise we keep on traversing the tree. Here is the algorithm of this approach:

• DEF DoesSumExist(root, k):
• hashSet = []
• RETURN DoesSumExistUsingSet(root, k, hashSet)

• DEF DoesSumExistUsingSet(node, k, hashSet):
• IF node == null
• RETURN FALSE
• IF hashSet has (k - node.val)
• RETURN TRUE
• hashSet.Add(node.val)
• RETURN DoesSumExistUsingSet(node.left, k hashSet) OR DoesSumExistUsingSet(node.right, k, hashSet)

You can see we are just traversing tree once in this approach and also the extra space could be less than number of elements in the tree. However HashSet could take more space than an array or list.

I am giving the implementation of Approach 2 and Approach 3.

Implementation in C#:

Approach 2: Flatten the BSTree to Sorted Array:

    public bool FindTarget(TreeNode root, int k) 

    {

        List<int> flattenBSTreeList = new List<int>();

        this.FlattenBSTree(root, flattenBSTreeList);

        return this.IsSumExist(flattenBSTreeList, k);

    }

    

    private void FlattenBSTree(TreeNode node, List<int> flattenBSTreeList)

    {

        if (node != null)

        {

            this.FlattenBSTree(node.left, flattenBSTreeList);

            flattenBSTreeList.Add(node.val);

            this.FlattenBSTree(node.right, flattenBSTreeList);

        }

    }

    private bool IsSumExist(List<int> flattenBSTreeList, int k)

    {

        int start = 0, end = flattenBSTreeList.Count - 1;

        while (start < end)

        {

            int currSum = flattenBSTreeList[start] + flattenBSTreeList[end];

            if (currSum == k)

            {

                return true;

            }

            else if (currSum < k)

            {

                ++start;

            }

            else

            {

                --end;

            }

        }

        return false;

    }

Approach 3: Using Hashing:

    public bool FindTarget(TreeNode root, int k) 

    {    

        HashSet<int> nodeValSet = new HashSet<int>();

        return this.IsSumExist(root, nodeValSet, k);

    }

    

    private bool IsSumExist(TreeNode node, HashSet<int> nodeValSet, int k)

    {

        if (node == null)

        {

            return false;

        }        

        if (nodeValSet.Contains(k - node.val))

        {

            return true;

        }

        nodeValSet.Add(node.val);        

        return this.IsSumExist(node.left, nodeValSet, k) || 

            this.IsSumExist(node.right, nodeValSet, k);

    }

Complexity: O(n) but preferred is approach 3 as it does only one traversal.

[LeetCode] Unique Binary Search Trees II

Problem: Given an integer n, return all the structurally unique BST's (binary search trees), which has exactly n nodes of unique values from 1 to n. Return the answer in any order.

Example:

Input: n = 3
Output: [[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

Input: n = 1
Output: [[1]]

Constraints:

• 1 <= n <= 8

Approach: The intuition is to take each number i from 1...n as root and then because we need to create BST, we know that left subtree will have numbers 1...i - 1 and right subtrees will have i + 1...n. With this intuition, here is our algorithm:

• DEFINE generate_tree (start, end)
• result = new list()
• IF start > end
• RETURN new List {null}
• FOR i = 1 TO n
• leftTrees = generate_tree (start, i - 1) // recursively make all left subtrees
• rightTrees = generate_tree (i + 1, end) // recursively make all right subtrees
• FOR j = 0 TO leftTrees.Length
• FOR k = 0 TO rightTrees.Length
• Node node = new Node(i)
• node.left =  leftTrees[j]
• node.right = rightTrees[k]
• result.Add(node)
• return result

Implementation in C#:

    public IList<TreeNode> GenerateTrees(int n) 

    {

        if (n <= 0)

        {

            return new List<TreeNode>();

        }

        return this.GenerateTrees(1, n);

    }

    

    private List<TreeNode> GenerateTrees(int start, int end)

    {

        List<TreeNode> result = new List<TreeNode>();

        if (start > end)

        {

            result.Add(null);

            return result;

        }

        for (int i = start; i <= end; ++i)

        {

            List<TreeNode> leftTrees = this.GenerateTrees(start, i - 1);

            List<TreeNode> rightTrees = this.GenerateTrees(i + 1, end);

            

            for (int j = 0; j < leftTrees.Count; ++j)

            {

                for (int k = 0; k < rightTrees.Count; ++k)

                {

                    TreeNode node = new TreeNode(i);

                    node.left =  leftTrees[j];

                    node.right = rightTrees[k];

                    result.Add(node);

                }

            }

        }     

        return result;

    }

Complexity: O(number of BSTs) = O(nth Catalan number) = O((2n)!/((n+1)!*n!))

[Google Question][LeetCode] Split BST

Problem: Given a Binary Search Tree (BST) with root node root, and a target value V, split the tree into two subtrees where one subtree has nodes that are all smaller or equal to the target value, while the other subtree has all nodes that are greater than the target value.  It's not necessarily the case that the tree contains a node with value V.

Additionally, most of the structure of the original tree should remain.  Formally, for any child C with parent P in the original tree, if they are both in the same subtree after the split, then node C should still have the parent P.

You should output the root TreeNode of both subtrees after splitting, in any order.

Example:

Input: root = [4,2,6,1,3,5,7], V = 2
Output: [[2,1],[4,3,6,null,null,5,7]]
Explanation:
Note that root, output[0], and output[1] are TreeNode objects, not arrays.

The given tree [4,2,6,1,3,5,7] is represented by the following diagram:

          4
        /   \
      2      6
     / \    / \
    1   3  5   7

while the diagrams for the outputs are:

          4
        /   \
      3      6      and    2
            / \           /
           5   7         1

Note:

• The size of the BST will not exceed 50.
• The BST is always valid and each node's value is different.

Approach: Let's take a hint from the question description. At any node there are two conditions:

1. curr_node.Value <= V: In that case we know that the whole left subtree of curr_node including the curr_node is going to be part of first half but there is possibility that there are few nodes in the right subtree of curr_node which belongs to first half and other nodes of right subtree belongs to the second half. That means we need to make a recursive call for the right subtree,
2. curr_node.Value > V: In this case we are sure that right subtree of curr_node including the curr_node is part of second half but we are not sure about left subtree yet. That means we need to make recursive call for left subtree.

If you understand the above two points the implementation is simple. Just have a look!

Implementation in C#:

    public TreeNode[] SplitBST(TreeNode root, int V) 

    {

        if (root == null)

        {

            return new TreeNode[] { null, null };

        }    

        if (root.val <= V)

        {

            TreeNode[] bsts = this.SplitBST(root.right, V);

            root.right = bsts[0];

            bsts[0] = root;

            return bsts;

        }

        else

        {

            TreeNode[] bsts = this.SplitBST(root.left, V);

            root.left = bsts[1];

            bsts[1] = root;

            return bsts;

        }

    }

Complexity: O(height of BST)

[Microsoft Question] Inorder Successor in Binary Search Tree

Problem: Given a binary search tree and a node in it, return the in-order successor of that node in the binary search tree. If the given node has no in-order successor in the tree, return null.

The successor of a node is the node with the smallest value greater than value of the given input node.

Example:

Input: Above tree, input = 6
Output: 8

Approach: We can use the similar approach which we used which we used to set the inorder successor of every node in Binary tree but that will take linear time as we are not using Binary Search Tree's property in this approach.

Let's make the solution efficient by using the BST's property. We can do preorder traversal here. There can be two conditions at every node:

1. curr_node.Value <= input.Value: In this case we just discard the left subtree of the curr_node.
2. curr_node.Value > input.Value: In this case we can discard the right subtree of curr_node, but if we see curr_node can also be a candidate of being a inorder successor of the input node.

With this understanding, look at the implementation to understand the whole solution.

Implementation in C#:

    public BinaryTreeNode InorderSuccessor(BinaryTreeNode input) 

    {

        if (this.Root == null)

        {

            return null;

        }

        BinaryTreeNode successor = null;

        BinaryTreeNode node = this.Root;

        while (node != null)

        {

            if (node.Value <= input.Value)

            {

                node = node.RightNode;

            }

            else

            {

                successor = node;

                node = node.LeftNode;

            }

        }

        return successor;

    }

Complexity: O(logn)

Convert Binary Search Tree to Greater Tree

Problem: Convert a Binary Search Tree to a Greater Tree such that every node's value of the original BST is changed to sum of original node's value and sum of all the values in BST which are greater than original node's value.

Example:

Input: The binary search tree in the above image with blue nodes.
Output: The values of node will be changed to the values in the rectangle box in the above image. 

Approach: We can use reverse Pre-Order traversal here (first right and then left) and keep the previous sum in the recursive calls. Here are the changes that we need to apply:

• previous_sum = previous_sum + node.Value
• node.Value = previous_sum

Implementation in C#:

        public void ToGreaterTree()

        {

            if (this.Root == null)

            {

                return;

            }

            int prevSum = 0;

            this.ToGreaterTree(this.Root, ref prevSum);

        }

        private void ToGreaterTree(BinaryTreeNode node, ref int prevSum)

        {

            if (node != null)

            {

                this.ToGreaterTree(node.RightNode, ref prevSum);

                prevSum += node.Value;

                node.Value = prevSum;

                this.ToGreaterTree(node.LeftNode, ref prevSum);

            }

        }

Complexity: O(n)

Remove all the nodes in BST which are not in a range

Problem: Given a binary search tree and a range [low, high] where low being the lowest and high being the highest boundaries of the range, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree. 

Example:

Input: low = 2, high = 3

Approach: We can use Pre Order traversal to solve this problem. Approach is straight forward and can be understood by just looking at the code.

Implementation in C#:

        public void TrimBST(int low, int high)

        {

            if (this.Root == null)

            {

                return;

            }

            this.Root = this.TrimBST(this.Root, low, high);

        }

        private BinaryTreeNode TrimBST(BinaryTreeNode node, int low, int high)

        {

            if (node == null)

            {

                return null;

            }

            if (node.Value > high)

            {

                return this.TrimBST(node.LeftNode, low, high);

            }            

            if (node.Value < low)

            {

                return this.TrimBST(node.RightNode, low, high);

            }

            node.LeftNode = this.TrimBST(node.LeftNode, low, high);

            node.RightNode = this.TrimBST(node.RightNode, low, high);

            return node;

        }

Complexity: O(n)

Delete a node of BST

Problem: Given a Binary Search Tree and a value key. Remove the node from tree whose value is equal to the given key.

Approach: You can refer the Binary Search Tree section for approach. I am just giving implementation in C#.

Implementation in C#:

        public void Remove(int key)

        {

            if (this.Root != null)

            {

                this.Root = this.RemoveNode(this.Root, key);

            }

        }

        private BinaryTreeNode RemoveNode(BinaryTreeNode node, int key)

        {

            if (node == null)

            {

                return null;

            }

            if (key < node.Value)

            {

                node.LeftNode = this.RemoveNode(node.LeftNode, key);

            }

            else if (key > node.Value)

            {

                node.RightNode = this.RemoveNode(node.RightNode, key);

            }

            else

            {

                if (node.RightNode == null)

                {

                    return node.LeftNode;

                }

                else if (node.LeftNode == null)

                {

                    return node.RightNode;

                }

                else 

                {

                    node.Value = this.FindMin(node.RightNode);

                    node.RightNode = this.RemoveNode(node.RightNode, node.Value);

                }

            }

            return node;

        }

        private int FindMin(BinaryTreeNode node)

        {

            while(node.LeftNode != null)

            {

                node = node.LeftNode;

            }

            return node.Value;

        }

Complexity: O(h) where h is height of the tree

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

Approach: We don't have to use bottom-up / Post order traversal approach here like we did in finding LCA of Binary Tree. We can use following property of BST to simplify it:

node.Left.Value < node.Value < node.Right.Value

So we can use top-bottom approach. At each node, we can have one of the following conditions:

1. Both of the input nodes' values are less than current node value. In this case we just have to go to current node's left and search there.
2. Both of the input nodes' values are greater than current node value. In this case we just have to go to current node's right and search there.
3. We got our node

Implementation in C#:

        public new BinaryTreeNode LowestCommonAncestor(BinaryTreeNode p, BinaryTreeNode q)

        {

            if (this.Root == null)

            {

                return null;

            }

            return this.LowestCommonAncestor(this.Root, p, q);

        }

        private new BinaryTreeNode LowestCommonAncestor(BinaryTreeNode node, BinaryTreeNode p, BinaryTreeNode q)

        {

            if (node == null)

            {

                return null;

            }

            if (node.Value < p.Value && node.Value < q.Value)

            {

                return this.LowestCommonAncestor(node.RightNode, p, q);

            }

            else if (node.Value > p.Value && node.Value > q.Value)

            {

                return this.LowestCommonAncestor(node.LeftNode, p, q);

            }

            else

            {

                return node;

            }

        }

Complexity: O(n)

Binary Search Tree Iterator

Problem: Implement an iterator over a binary search tree (BST). Your iterator should perform following operations -

1. Next - Return the next smallest number in the BST.
2. HasNext - Check if there is any element.

Approach: We can see that we need a inorder traversal here. What we can do is we can store all the nodes in an array using inorder traversal but that will increase the space a lot. If we want to reduce space then we can actually have a member say k and can return kth smallest node by doing inorder traversal every time when somebody calls Next.

Now if we go with recursion approach of inorder traversal, we always have to start from root but if we use the stack approach, we can do little better both in terms of time and space.

    public class BSTIterator

    {

        public BSTIterator(BinaryTreeNode root)

        {

            this.stack = new Stack<BinaryTreeNode>();

            this.PushTillLeftMost(root);

        }

        public int Next()

        {

            BinaryTreeNode node = stack.Pop();

            if (node.RightNode!= null)

            {

                this.PushTillLeftMost(node.RightNode);

            }

            return node.Value;

        }

        public bool HasNext()

        {

            return stack.Count > 0;

        }

        private void PushTillLeftMost(BinaryTreeNode node)

        {

            while (node != null)

            {

                stack.Push(node);

                node = node.LeftNode;

            }

        }

        private Stack<BinaryTreeNode> stack;

    }

[LeetCode] Recover the tree without changing its structure.

Problem: You are given the root of a binary search tree (BST), where the values of exactly two nodes of the tree were swapped by mistake. Recover the tree without changing its structure.

Example:

Input: root = [1,3,null,null,2]
Output: [3,1,null,null,2]
Explanation: 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.

Input: root = [3,1,4,null,null,2]
Output: [2,1,4,null,null,3]
Explanation: 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.

Approach: Use inorder traversal to detect nodes to be swapped.

Implementation in C#:

    public void RecoverTree(TreeNode root) 

    {

        if (root == null)

        {

            return;

        }

        TreeNode first = null, second = null, prev = null;

        this.RecoverTreeFindNodes(root, ref first, ref second, ref prev);

        int temp = first.val;

        first.val = second.val;

        second.val = temp;

    }

    

    private void RecoverTreeFindNodes(TreeNode node, ref TreeNode first, ref TreeNode second, ref TreeNode prev)

    {

        if (node != null)

        {

            this.RecoverTreeFindNodes(node.left, ref first, ref second, ref prev);

            

            if (prev != null && node.val <= prev.val)

            {

                if (first == null)

                {

                    first = prev;

                }

                second = node;

            }

            prev = node;

            this.RecoverTreeFindNodes(node.right, ref first, ref second, ref prev);

        }

    }

Complexity: O(n)

[Google] Construct BST from given preorder traversal

Problem: Construct BST from given preorder traversal.

Approach: Straight forward to understand. Please look at the implementation for more understanding.

Implementation in C#:

    public TreeNode BstFromPreorder(int[] preorder) 

    {

        int index = 0;

        return this.BstFromPreorder(preorder, ref index, preorder[0], int.MinValue, int.MaxValue);

    }

    

    private TreeNode BstFromPreorder(int[] preorder, ref int index, int num, int min, int max)

    {

        if (index >= preorder.Length)

        {

            return null;

        }

        TreeNode node = null;

        if (num > min && num < max)

        {

            node = new TreeNode(num);

            ++index;

            if (index < preorder.Length)

            {

                node.left = BstFromPreorder(preorder, ref index, preorder[index], min, num);

            }

            

            if (index < preorder.Length)

            {

                node.right = BstFromPreorder(preorder, ref index, preorder[index], num, max);

            }

        }

        

        return node;

    }

Complexity: O(n)

Binary Search Tree

The property that makes a Binary Tree into Binary Search Tree is that for every node, X, in the tree, the values of all the keys in the left subtree are smaller than the key value in X and the values of all the keys in the right subtree are larger than or equal to key value in X.

Example of a Binary Search Tree is:

The class to implement Binary Search Tree :

// Node class

template < class Etype >
class TreeNode
{
public:
        Etype element;
        TreeNode* Left;
        TreeNode* Right;
        TreeNode( Etype e = 0, TreeNode* l = NULL, TreeNode* r = NULL) : 
        element ( e), left ( l ), right ( r ) { }
        friend int height ( TreeNode *T);
        friend void inOrderTraversal ( TreeNode *T);
        friend void preOrderTraversal ( TreeNode *T);
        friend void postOrderTraversal ( TreeNode *T);
        friend class BinarySearchTree < Etype >;
};

// Binary Search Tree Class

template<class Etype>
class BinarySearchTree
{
public: 
         BinarySearchTree ( ) : Root ( NULL ) { }
         void insert ( const Etype & x ) {  insert ( x, root ); }
         void remove ( const Etype& x ) { Remove (  x, root ); }
private:
         void insert ( const Etype& x, TreeNode<Etype>* & T );
         void remove ( const Etype& x, TreeNode<Etype>* & T);
         TreeNode *root;
};

Height:

int height ( TreeNode *T)
{
        return ( T ? 1 + Max ( height ( T-> left ), height ( T-> right ) ) : 0 ) ; 
}

Inorder Traversal:

void inOrderTraversal ( TreeNode *T)
{
       if ( T )
       {
                inOrderTraversal ( T-> left );
                cout<< T-> element;
                inOrderTraversal ( T-> right);
        }
}

Preorder Traversal:


void preOrderTraversal ( TreeNode *T)
{
       if ( T )
       {
                cout<< T-> element;
                preOrderTraversal ( T-> left );
                preOrderTraversal ( T-> right);

        }

}

Postorder Traversal:


void postOrderTraversal ( TreeNode *T)
{
       if ( T )
       {
                postOrderTraversal ( T-> left );
                postOrderTraversal ( T-> right);
                cout<< T-> element;
        }

}




Insert:

Following image shows how to insert an element in Binary Search Tree:

Following is the implementation of insert( ) function:

template < class Etype >
void BinarSearchTree< Etype > :: insert ( const Etype & x, TreeNode<Etype> * & T)
{
         if ( T = = NULL )
                 T = new TreeNode<Etype> ( x );
        else
        {
                 if ( x < T -> element )
                          insert ( x, T->left );
                 else if ( x > T-> element)
                          insert ( T-> right )
         }
}


Remove:

Following image shows how to remove an element in Binary Search Tree:

Following is the implementation of remove( ) function:

template < class Etype >
void BinarySearchTree< Etype > :: remove ( const Etype & x, TreeNode<Etype> * & T)
{
        TreeNode<Etype> *tmpCell;
   
        if ( T = = NULL )
                 cout << " Element Not Found ";
        else if ( x < T-> element )
                 remove ( x, T-> left );
        else if ( x > T-> element )
                 remove ( x, T-> right );
        else       // element found
        {
                  if ( T-> left != NULL && T -> right != NULL )
                  {
                            tmpCell = findMin ( T-> right );   // Minimum element
                            T-> element = tmpCell -> element;
                            remove ( T->element, T->right );
                  }
                 else
                 {
                          tmpCell = T;
                          if ( T-> left)
                                     T = T-> left;
                         else if ( T-> right )
                                     T = T-> right;
                         delete tmpCell;
                  }
        }
}

Google Question: Find nth minimum in Binary Search Tree.

1. Without extra field in Node structure --

Do inorder traversal and count number of node visited. When count is equal to n return the node.
void BSTree::findNthElem(Node* node, int& n, int& retval)
{
if(!node && n)
retval = -1;
else if(n)
{
findNthElem(node->left, n, retval);
if(n)
{
n = n - 1;
if(n == 0)
retval = node->data;
findNthElem(node->right, n, retval);
}
}
}