Problem: Given the root of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.
Return the maximum product of the sums of the two subtrees. Since the answer may be too large, return it modulo 10^9 + 7.
Note that you need to maximize the answer before taking the mod and not after taking it.
Example:
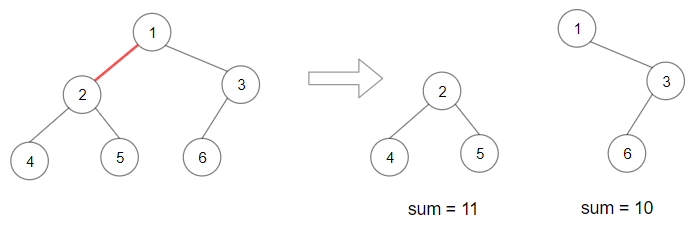
Input: root = [1,2,3,4,5,6] Output: 110 Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)
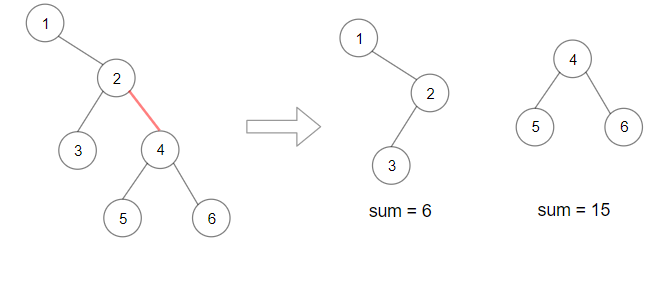
Input: root = [1,null,2,3,4,null,null,5,6] Output: 90 Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)
Input: root = [2,3,9,10,7,8,6,5,4,11,1] Output: 1025
Input: root = [1,1] Output: 1
Constraints:
- The number of nodes in the tree is in the range [2, 5 * 104].
- 1 <= Node.val <= 104
Approach: We need to look at the problem in this way, say if we know the total sum of the tree and then at every node we can check if the sum of current sub tree * (total sum - sum of current sub tree) is greater than maximum product then we reassign the maximum product to sum of current sub tree * (total sum - sum of current sub tree).
Now to get the total sum we can apply any traversal and get the total sum but to get the sum of current sub tree we need to use post order traversal. In that way we can get our answer but if we see we need to traverse the tree 2 times. Let's see if we can do better.
If we use post order traversal to calculate the total sum then we can basically use a HashSet / List to store all the intermediate sums. Now we just need to visit every element in HashSet/List and do the following:
maxProduct = MAX (maxProduct, setElement * (total sum - setElement))
I think traversing a List / HashSet is much faster than traversing a binary tree. However the time complexity remains same and second approach will require more space so I would like to go with 1st approach.
Implementation in C#:
Approach 1:
public int MaxProduct(TreeNode root)
{
int mod = (int) 1e9 + 7;
long totalSum = this.GetBinaryTreeSum(root);
long maxProduct = 0;
this.GetMaxProduct(root, totalSum, ref maxProduct);
return (int) (maxProduct % mod);
}
private long GetMaxProduct(TreeNode node, long totalSum, ref long maxProduct)
{
if (node == null)
{
return 0;
}
long sumOfCurrSubTree = this.GetMaxProduct(node.left, totalSum, ref maxProduct) +
this.GetMaxProduct(node.right, totalSum, ref maxProduct) + node.val;
long currProduct = sumOfCurrSubTree * (totalSum - sumOfCurrSubTree);\
maxProduct = Math.Max(currProduct, maxProduct);
return sumOfCurrSubTree;
}
private long GetBinaryTreeSum(TreeNode node)
{
if (node == null)
{
return 0;
}
return node.val + this.GetBinaryTreeSum(node.left) + this.GetBinaryTreeSum(node.right);
}
Approach 2:
public int MaxProduct(TreeNode root)
{
int mod = (int) 1e9 + 7;
HashSet<long> allSubTreeSums = new HashSet<long>();
long totalSum = this.GetBinaryTreeSumAndCollectAllSum(root, allSubTreeSums);
return (int) (this.GetMaxProduct(totalSum, allSubTreeSums) % mod);
}
private long GetMaxProduct(long totalSum, HashSet<long> allSubTreeSums)
{
long maxProduct = 0;
foreach (long sum in allSubTreeSums)
{
maxProduct = Math.Max(maxProduct, (totalSum - sum) * sum);
}
return maxProduct;
}
private long GetBinaryTreeSumAndCollectAllSum(TreeNode node, HashSet<long> allSubTreeSums)
{
if (node == null)
{
return 0;
}
long currSum = this.GetBinaryTreeSumAndCollectAllSum(node.left, allSubTreeSums) +
this.GetBinaryTreeSumAndCollectAllSum(node.right, allSubTreeSums) +
node.val;
allSubTreeSums.Add(currSum);
return currSum;
}
Complexity: O(n) for both approaches.
No comments:
Post a Comment