Problem: Given a Binary Tree, find its Boundary Traversal. The traversal should be in the following order:
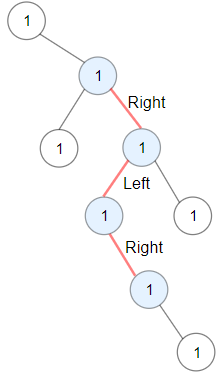
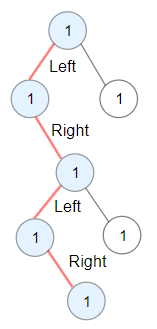
- Left boundary nodes: defined as the path from the root to the left-most node ie- the leaf node you could reach when you always travel preferring the left subtree over the right subtree.
- Leaf nodes: All the leaf nodes except for the ones that are part of left or right boundary.
- Reverse right boundary nodes: defined as the path from the right-most node to the root. The right-most node is the leaf node you could reach when you always travel preferring the right subtree over the left subtree. Exclude the root from this as it was already included in the traversal of left boundary nodes.
Note: If the root doesn't have a left subtree or right subtree, then the root itself is the left or right boundary.
Example:
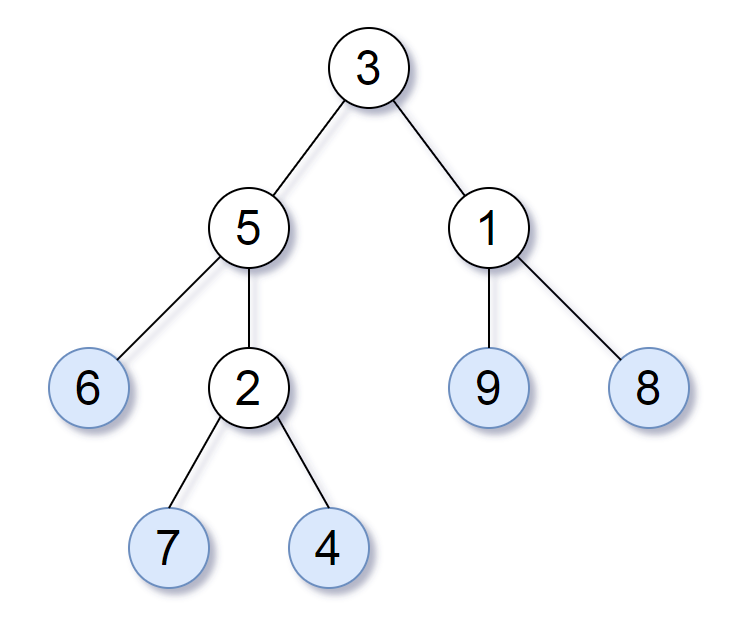
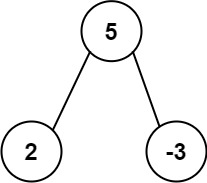
Input: 1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9 Output: 1 2 4 8 9 6 7 3 Explanation:
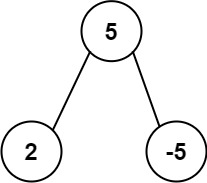
Input: 1 / 2 / \ 4 9 / \ \ 6 5 3 / \ 7 8 Output: 1 2 4 6 5 7 8 Explanation:As you can see we have not taken the right subtree.
Approach: We can solve this problem in four steps given the nature of the problem:
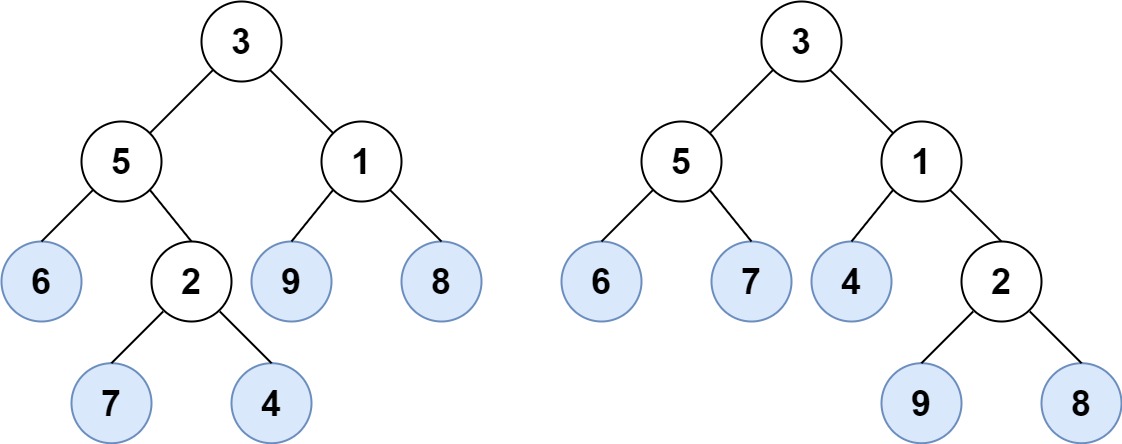
- Add root to result.
- Preorder traversal of left subtree. If left child is available then do not go for right child. Ignore the leaves.
- Inorder traversal of leaves if root is not leaf.
- Postorder traversal of right subtre. If right child is available then do not go for left child. Ignore the leaves.
Implementation in C#:
class BinaryTreeNode
{
public BinaryTreeNode Left {get; set;}
public BinaryTreeNode Right {get; set;}
public int Value {get; set;}
public BinaryTreeNode(int val,
BinaryTreeNode left = null,
BinaryTreeNode right = null)
{
this.Left = left;
this.Right = right;
this.Value = val;
}
}
class BinaryTree
{
public List<int> BoundaryTraversal()
{
List<int> result = new List<int>();
if (this.Root == null)
{
return result;
}
result.Add(this.Root.Value);
this.TraverseLeftBoundary(this.Root.Left, result);
// Avoid leaf traversing if root itself is leaf
if (this.Root.Left != null || this.Root.Right != null)
{
this.TraverseLeaves(this.Root, result);
}
this.TraverseRightBoundary(this.Root.Right, result);
return result;
}
private void TraverseLeftBoundary(BinaryTreeNode node,
List<int> result)
{
if (node == null ||
(node.Left == null && node.Right == null))
{
return;
}
if (node.Left != null)
{
result.Add(node.Value);
this.TraverseLeftBoundary(node.Left, result);
}
else
{
result.Add(node.Value);
this.TraverseLeftBoundary(node.Right, result);
}
}
private void TraverseLeaves(BinaryTreeNode node,
List<int> result)
{
if (node == null)
{
return;
}
this.TraverseLeaves(node.Left, result);
if (node.Left == null && node.Right == null)
{
result.Add(node.Value);
}
this.TraverseLeaves(node.Right, result);
}
private void TraverseRightBoundary(BinaryTreeNode node,
List<int> result)
{
if (node == null ||
(node.Left == null && node.Right == null))
{
return;
}
if (node.Right != null)
{
this.TraverseRightBoundary(node.Right, result);
result.Add(node.Value);
}
else
{
this.TraverseRightBoundary(node.Left, result);
result.Add(node.Value);
}
}
public BinaryTreeNode Root {get; set;}
}
Complexity: O(n)