[LeetCode] Count Good Nodes in Binary Tree

Problem: Given a binary tree root, a node X in the tree is named good if in the path from root to X there are no nodes with a value greater than X.

Return the number of good nodes in the binary tree.

Example:

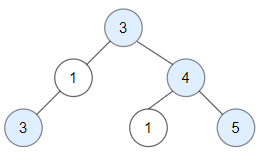
Input: root = [3,1,4,3,null,1,5]
Output: 4
Explanation: Nodes in blue are good.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.

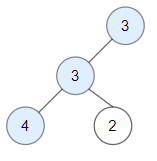
Input: root = [3,3,null,4,2]
Output: 3
Explanation: Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.

Input: root = [1]
Output: 1
Explanation: Root is considered as good.

Constraints:

• The number of nodes in the binary tree is in the range [1, 10^5].
• Each node's value is between [-10^4, 10^4].

Approach: We can use Preorder traversal here. Basically in each recursive call, we maintain the maximum number from root to current node and if we find the value at current node is greater than or equal to the max number we maintained then we increase the count of good nodes by 1 (max will also be updated) otherwise the count remains same.

 

Implementation in C#:

        public int GoodNodes(TreeNode root)

    {

        if (root == null)

        {

            return 0;

        }

        return this.GetNumOfGoodNodes(root, int.MinValue);

    }

    private int GetNumOfGoodNodes(TreeNode node, int maxOfPath)

    {

        if (node == null)

        {

            return 0;

        }

        int currVal = 0;

        if (node.val >= maxOfPath)

        {

            currVal = 1;

            maxOfPath = node.val;

        }

        return currVal +

               this.GetNumOfGoodNodes(node.left, maxOfPath) +

               this.GetNumOfGoodNodes(node.right, maxOfPath);

    }

Complexity: O(n)