Construct Binary Tree from Preorder and Inorder Traversal

Problem: Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

Example:

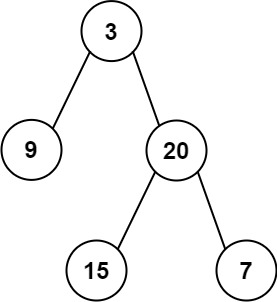
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Input: preorder = [-1], inorder = [-1]
Output: [-1]

Constraints:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder and inorder consist of unique values.
• Each value of inorder also appears in preorder.
• preorder is guaranteed to be the preorder traversal of the tree.
• inorder is guaranteed to be the inorder traversal of the tree

Approach: We can solve this problem recursively. Let's see how. We will build the tree in preorder manner. That means we will have three steps:

1. Build root: How we will get the value of the root? The first value of preorder array will be root's value, right so we are good here.

2. Build root's left subtree recursively: Now how to determine the inorder and preorder arrays for left subtree? Now let's see how our inorder array looks like:

[...left... root ...right...]

Right, so inorder subarray for the left subtree is  [0.....rootValIndex - 1] right? Now instead of 0 we will use inorderStart as it won't be always 0 as it's a recursive method so here is the inorder array start and end:

• leftInorderStart = inorderStart
• leftInorderEnd = rootValIndex - 1

Now that inorder array start and end are settled, let' see how our preorder array looks like:

[root ...left... ...right...]

So preorder subarray left subtree is [0 + 1 ... rightSubtreeStartIndex - 1]. Again instead of 1 we will use preOrderStart + 1 for leftPreorderStart, given the recursive nature but how we can calculate rightSubtreeStartIndex - 1 which will be leftPreorderEnd?

One thing is clear number of elements in leftInorderSubArray should be equal to leftPrerderSubArray. That means:

leftPreorderEnd - leftPreorderStart + 1 = leftInorderEnd - leftInorderStart  + 1

=> leftPreorderEnd - leftPreorderStart = leftInorderEnd - leftInorderStart

=> leftPreorderEnd = leftInorderEnd - leftInorderStart + leftPreorderStart;

So now we can say:

• leftPreorderStart = preorderStart + 1
• leftPreorderEnd = leftInorderEnd - leftInorderStart + leftPreorderStart;

3. Build root's right subtree recursively: Let's first see about the rightInorderArray start and end. Let's recall how our inorder array looks like:

[...left... root ...right...]

Looking at the array we can safely say:

• rightInorderStart = rootValIndex + 1
• rightInorderEnd = inorderEnd

Now let's look at rightPreorderArray start and end by looking at the preorder array:

[root ...left... ...right...]

So we can say:

• rightPreorderStart = leftPreorderEnd + 1
• rightPreorderEnd = preorderEnd

Once we calculated all these 8 indices, we can use recursion to build the tree.

Implementation in C#:

    public TreeNode BuildTree(int[] preorder, int[] inorder)

    {

        int length = preorder?.Length ?? 0;

        if (length == 0)

        {

            return null;

        }

        var inorderIndexMap = this.BuildIndexMap(inorder);

        return this.BuildTree(preorder,

                              inorder,

                              0,

                              length - 1,

                              0,

                              length - 1,

                              inorderIndexMap);

    }

    private TreeNode BuildTree(int[] preorder,

                               int[] inorder,

                               int preStart,

                               int preEnd,

                               int inStart,

                               int inEnd,

                               Dictionary<int, int> inorderIndexMap)

    {

        if (inStart > inEnd)

        {

            return null;

        }

        int nodeVal = preorder[preStart];

        int nodeValIndex = inorderIndexMap[nodeVal];

        TreeNode node = new TreeNode(nodeVal);

        int leftInStart = inStart;

        int leftInEnd = nodeValIndex - 1;

        int leftPreStart = preStart + 1;

        int leftPreEnd = leftInEnd - leftInStart + leftPreStart;

        node.left = this.BuildTree(preorder,

                                   inorder,

                                   leftPreStart,

                                   leftPreEnd,

                                   leftInStart,

                                   leftInEnd,

                                   inorderIndexMap);

        int rightInStart = nodeValIndex + 1;

        int rightInEnd = inEnd;

        int rightPreStart = leftPreEnd + 1;

        int rightPreEnd = preEnd;

        node.right = this.BuildTree(preorder,

                                    inorder,

                                    rightPreStart,

                                    rightPreEnd,

                                    rightInStart,

                                    rightInEnd,

                                    inorderIndexMap);

        return node;

    }

    private Dictionary<int, int> BuildIndexMap(int[] nums)

    {

        var indexMap = new Dictionary<int, int>();

        for (int i = 0; i < nums.Length; ++i)

        {

            indexMap[nums[i]] = i;

        }

        return indexMap;

    }

Complexity: O(n)