[LeetCode] Search an element in a Sorted Matrix

Problem: You are given an m x n integer matrix matrix with the following two properties:

• Each row is sorted in non-decreasing order.
• The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Example:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

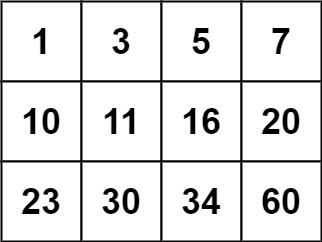
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Approach: The best approach would be if we flatter this 2D array into a 1D array and do a binary search but if we actually flatten it then we already have consumed O(m * n) time and there will be no optimization as a linear search can be performed in this time.

Let's say we won't actually flatten it and we will try to map 1D array index into 2D array. Let's see the binary search indices:

1. low = 1D - 0, 2D - (0, 0)
2. high = 1D - m * n - 1, 2D (m - 1, n - 1)
3. mid = this is little tricky, any index i can be mapped to following index in 2D
1. row = i / n (cols)
2. col = i % n (cols) 

In this way we can apply the binary search in 2D matrix.

Implementation in C#:

    public bool SearchMatrix(int[][] matrix, int target)

    {

        int rows = matrix?.Length ?? 0;

        if (rows == 0)

        {

            return false;

        }

        int cols = matrix[0].Length;

        int low = 0, high = rows * cols - 1;

        while (low <= high)

        {

            int mid = low + (high - low) / 2;

            int row = mid / cols;

            int col = mid % cols;

            if (matrix[row][col] == target)

            {

                return true;

            }

            else if (matrix[row][col] < target)

            {

                low = mid + 1;

            }

            else

            {

                high = mid - 1;

            }

        }

        return false;

    }

Complexity: O(log(m * n))