Construct a Binary Tree from Postorder and Inorder Traversal

Problem: Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.

Example:

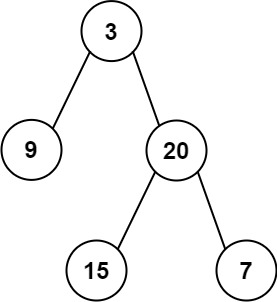
Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
Output: [3,9,20,null,null,15,7]

Input: inorder = [-1], postorder = [-1]
Output: [-1]

Constraints:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder and postorder consist of unique values.
• Each value of postorder also appears in inorder.
• inorder is guaranteed to be the inorder traversal of the tree.
• postorder is guaranteed to be the postorder traversal of the tree.

Approach: Like we build Binary Tree from Preorder and Inorder, we are going to build Binary tree using Postorder and Inorder recursively in preorder way. The recursive method will be looking like following:

BuildTree(inorder, postorder, inStart, inEnd, postStart, postEnd) 

Now we will build left and right subtree recursively:

• root.left = BuildTree(inorder, postorder, leftInStart, leftInEnd, leftPostStart, leftPostEnd) 
• root.right = BuildTree(inorder, postorder, rightInStart, rightInEnd, rightPostStart, rightPostEnd)

Now the problem is about finding 8 params which are leftInStart, leftInEnd, leftPostStart, leftPostEnd, rightInStart, rightInEnd, rightPostStart, rightPostEnd.

Before we go into finding the above values. First let's see how to find the root value. Let's look at how Postorder array looks like:

[...left... ...right... root]

so that means we can safely say the value at the end will be root value which is postorder[postEnd]. To find the above 8 values, we also need to see how inorder array looks like:

[...left... root ...right...]

Now let's try to find these values by looking at the both postorder and inorder array structure:

1. leftInStart: inStart
2. leftInEnd: rootIndex - 1 (root index we can find by search root value in inorder array)
3. leftPostStart: postStart
4. leftPostEnd: ???
5. rightInStart: rootIndex + 1
6. rightInEnd: inEnd
7. rightPostStart: leftPostEnd + 1
8. leftPostEnd: postEnd - 1

The only remaining thing to find leftPostEnd. We know the number of elements in the left inorder array and left postorder array are same so we can say:

leftPostEnd - leftPostStart + 1 = leftInEnd - leftInStart + 1

=> leftPostEnd - leftPostStart = leftInEnd - leftInStart

=> leftPostEnd = leftInEnd - leftInStart + leftPostStart  

That's all!

Implementation in C#:

    public TreeNode BuildTree(int[] inorder, int[] postorder)

    {

        int length = inorder?.Length ?? 0;

        if (length == 0)

        {

            return null;

        }

        var inorderIndexMap = this.BuildIndexMap(inorder);

        return this.BuildTree(inorder,

                              postorder,

                              0,

                              length - 1,

                              0,

                              length - 1,

                              inorderIndexMap);

    }

    private TreeNode BuildTree(int[] inorder,

                               int[] postorder,

                               int inStart,

                               int inEnd,

                               int postStart,

                               int postEnd,

                               Dictionary<int, int> inorderIndexMap)

    {

        if (inStart > inEnd)

        {

           

            return null;

        }

        int nodeVal = postorder[postEnd];

        int nodeValIndex = inorderIndexMap[nodeVal];

        TreeNode node = new TreeNode(nodeVal);

        int leftInStart = inStart;

        int leftInEnd = nodeValIndex - 1;

        int leftPostStart = postStart;

        int leftPostEnd = leftInEnd - leftInStart + leftPostStart;

        node.left = this.BuildTree(inorder,

                                   postorder,

                                   leftInStart,

                                   leftInEnd,

                                   leftPostStart,

                                   leftPostEnd,

                                   inorderIndexMap);

        int rightInStart = nodeValIndex + 1;

        int rightInEnd = inEnd;

        int rightPostStart = leftPostEnd + 1;

        int rightPostEnd = postEnd - 1;

        node.right = this.BuildTree(inorder,

                                    postorder,

                                    rightInStart,

                                    rightInEnd,

                                    rightPostStart,

                                    rightPostEnd,

                                    inorderIndexMap);

        return node;

    }

    private Dictionary<int, int> BuildIndexMap(int[] nums)

    {

        var indexMap = new Dictionary<int, int>();

        for (int i = 0; i < nums.Length; ++i)

        {

            indexMap[nums[i]] = i;

        }

        Console.WriteLine("Building Map Done");

        return indexMap;

    }

Complexity: O(n)