Problem: Given the root of a binary tree, return the number of uni-value subtrees. A uni-value subtree means all nodes of the subtree have the same value.
Example:
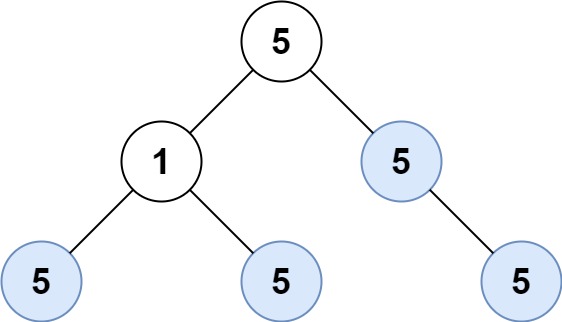
Input: root = [5,1,5,5,5,null,5] Output: 4
Approach: The basic here is to understand what is a uni-value subtree. Given a node in the tree is a uni-value subtree if it meets one of the following criteria:
- The node has no children.
- All of the node's children are uni-value subtrees, and the node and its children all have the same value.
So if you see we need to check first if children are uni-value or not then only we can decide whether current node is uni-value or not. This tells us that we can use Post-Order traversal here to solve this question. The basic check is:
If Left subtree is uni-val and Right subtree is uni-val then a node is uni-val if node.Value == node.Left.Value == node.Right.Value.
With a few boundary condition check we are good here. You can look at the implementation to see the boundary conditions.
Implementation in C#:
public int CountUnivalSubtrees()
{
int count = 0;
IsUnivalSubtree(this.Root, ref count);
return count;
}
private bool IsUnivalSubtree(BinaryTreeNode node, ref int count)
{
if (node == null)
{
return true;
}
if (node.LeftNode == null && node.RightNode == null)
{
++count;
return true;
}
bool leftUnival = this.IsUnivalSubtree(node.LeftNode, ref count);
bool rightUnival = this.IsUnivalSubtree(node.RightNode, ref count);
if (leftUnival && rightUnival)
{
if (node.LeftNode != null && node.RightNode != null && node.LeftNode.Value != node.RightNode.Value)
{
return false;
}
int compareVal = node.LeftNode?.Value ?? node.RightNode.Value;
if (node.val == compareVal)
{
++count;
return true;
}
}
return false;
}
Complexity: O(n)
No comments:
Post a Comment