[Amazon Question] Maximum Average Subtree

Problem: Given the root of a binary tree, find the maximum average value of any subtree of that tree. 

A subtree of a tree is any node of that tree plus all its descendants. The average value of a tree is the sum of its values, divided by the number of nodes.

Example:

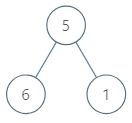
Input: Input = [5,6,1]
Output: 6
Explanation: 
For the subtree with root as 5, the average is (5 + 6 + 1) / 3 = 4
For the subtree with root as 6, the average is 6 / 1 = 6 and similarly for subtree with root as 1, the average is 1.
The answer is 6 as it is the maximum of all the above 3 averages.

Approach: We can use post-order traversal here as if we go by bottom-up approach, we will get the average at each and every node and then we can just store the maximum of all the averages. We need to write a function which will return the sum and the number of nodes (of the subtree) but we can have a ref parameter which can then be used for maintaining the maximum average.

Implementation in C#:

    public double MaximumAverageSubtree()

    {

        if (this.Root == null)

        {

            return 0;

        }

        double maxAverage = 0;        

        this.MaximumAverageSubtree(this.Root, ref maxAverage);

        return maxAverage;

    }

    

    private double[] MaximumAverageSubtree(BinaryTreeNode node, ref double maxAverage)

    {

        if (node == null)

        {

            return new double[] {0, 0};

        }

        double[] leftSumAndCount = this.MaximumAverageSubtree(node.LeftNode, ref maxAverage);

        double[] rightSumAndCount = this.MaximumAverageSubtree(node.RightNode, ref maxAverage);

        double sum = leftSumAndCount[0] + rightSumAndCount[0] + node.Value;

        double count = leftSumAndCount[1] + rightSumAndCount[1] + 1;

        double average = sum / count;

        if (average > maxAverage)

        {

            maxAverage = average;

        }        

        return new double[] {sum, count};

    }

Complexity: O(n)