[LeetCode] Most Frequent Subtree Sum

Problem: Given the root of a binary tree, return the most frequent subtree sum. If there is a tie, return all the values with the highest frequency in any order.

The subtree sum of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).

Example:

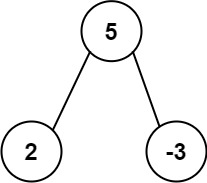
Input: root = [5,2,-3]
Output: [2,-3,4]

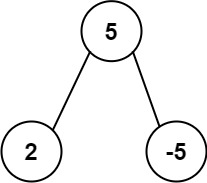
Input: root = [5,2,-5]
Output: [2]

Approach: We can use Preorder traversal here to solve this question. Approach is straight forward, can be understood easily by just looking at the implementation.

Implementation in C#:

    public int[] FindFrequentTreeSum(TreeNode root) 

    {

        if (root == null)

        {

            return null;

        }

        Dictionary<int, int> sumFreqMap = new Dictionary<int, int>();

        this.FindFrequentTreeSumPreOrder(root, sumFreqMap);

        HashSet<int> result = new HashSet<int>();

        int maxFreq = 0;

        foreach (var sumItem in sumFreqMap)

        {

            if (maxFreq < sumItem.Value)

            {

                result.Clear();

                result.Add(sumItem.Key);

                maxFreq = sumItem.Value;

            }

            else if (maxFreq == sumItem.Value)

            {

                result.Add(sumItem.Key);

            }

        }

        return result.ToArray();

    }

    

    public int FindFrequentTreeSumPreOrder(TreeNode node, Dictionary<int, int> sumFreqMap)

    {

        if (node == null)

        {

            return 0;

        }

        if (node.left == null && node.right == null)

        {

            if (!sumFreqMap.ContainsKey(node.val))

            {

                sumFreqMap[node.val]  = 0;

            }

            ++sumFreqMap[node.val];

            return node.val;

        }

        int leftSum = FindFrequentTreeSumPreOrder(node.left, sumFreqMap);

        int rightSum = FindFrequentTreeSumPreOrder(node.right, sumFreqMap);

        int subTreeSum = node.val + leftSum + rightSum;

        if (!sumFreqMap.ContainsKey(subTreeSum))

        {

            sumFreqMap[subTreeSum]  = 0;

        }

        ++sumFreqMap[subTreeSum];

        return subTreeSum;

    }

Complexity: O(n)