[LeetCode] Reorder Routes to Make All Paths Lead to the City Zero

Problem: There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.

Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi.

This year, there will be a big event in the capital (city 0), and many people want to travel to this city.

Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.

It's guaranteed that each city can reach city 0 after reorder.

Example:

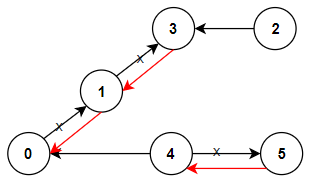
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
Output: 2
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Constraints:

• 2 <= n <= 5 * 104
• connections.length == n - 1
• connections[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi

Approach: This is clearly a graph as it is already mentioned in the question. Now the intuition is simple all the outgoing edges from 0 must be reversed so that there is a path to reach 0 from every city because it is given that there is only one path between two cities.

Now once the edges from 0 is reversed. We need to do the same for cities directly connected to 0 as there must be incoming path to every city x which is directly connected to 0 from every city directly connected to x, Right? See from example:

0 -> x -> y. We have reversed the path from 0 to x so now graph looks like 0 <- x -> y. How somebody will reach from city y to 0? We need to reverse the path x -> y so that the way now is 0 <- x <- y.

We will keep doing it recursively. With this intuition we can solve this problem using DFS but there are still some problems. Let's see it by example -

0 <- x -> y. As per our graph, there is no outgoing edge from 0 to x so we won't do anything and will return count as 0 as there is no neighbour of 0 given it's directed graph but we can see we have to reverse x -> y path. That means we must have incoming edges too in our graph.

Now the problem is if we store incoming edges how we will come to know if it is incoming edge and I should not reverse it? We can store the original edges in a set and compare before incresasing the count of edges to reverse but what I am doing it in my implementation is that I am pushing negative of city value to identify it given the cities are in range from 0 to n - 1.

Another problem is in case of outgoing edge to node's parent.We should not increase the count in case the connected city or neighbour city is it's parent, right. Consider this example:

0 -> 1 <- 2

Here we will have an positive edge from 2 -> 1 and as per our logice we will increase the count but it should not be the case. To avoid it we just need to check if the edge is ougoing to it's parent itself. Please note that this is happening because we are pushing incoming edges too in our graph.  

Hopefully it's clear now. 

Implementation in C#:

    public int MinReorder(int n, int[][] connections)

    {

        if (n <= 1)

        {

            return 0;

        }

        var cityGraph = this.GenerateCityGraph(connections);

        HashSet<int> visited = new HashSet<int>();

        return this.MinReorderDFS(cityGraph, 0, -1, visited);

    }

    private int MinReorderDFS(Dictionary<int, List<int>> cityGraph,

                              int currCity,

                              int parentCity,

                              HashSet<int> visited)

    {

        if (visited.Contains(currCity))

        {

            return 0;

        }

        visited.Add(currCity);

        int count = 0;

        if (cityGraph.ContainsKey(currCity))

        {

            foreach (int city in cityGraph[currCity])

            {

                if (city > 0 && city != parentCity)

                {

                    ++count;

                }

                count += this.MinReorderDFS(cityGraph,

                                            Math.Abs(city),

                                            currCity,

                                            visited);

            }

        }

        return count;

    }

    private Dictionary<int, List<int>> GenerateCityGraph(int[][] connections)

    {

        var cityGraph = new Dictionary<int, List<int>>();

        foreach (var connection in connections)

        {

            if (!cityGraph.ContainsKey(connection[0]))

            {

                cityGraph[connection[0]] = new List<int>();

            }

            cityGraph[connection[0]].Add(connection[1]);

            if (!cityGraph.ContainsKey(connection[1]))

            {

                cityGraph[connection[1]] = new List<int>();

            }

            cityGraph[connection[1]].Add(-connection[0]);

        }

        return cityGraph;

    }

Complexity: O(n)