Delete Node in a BST

Problem: Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

1. Search for a node to remove.
2. If the node is found, delete the node.

Example:

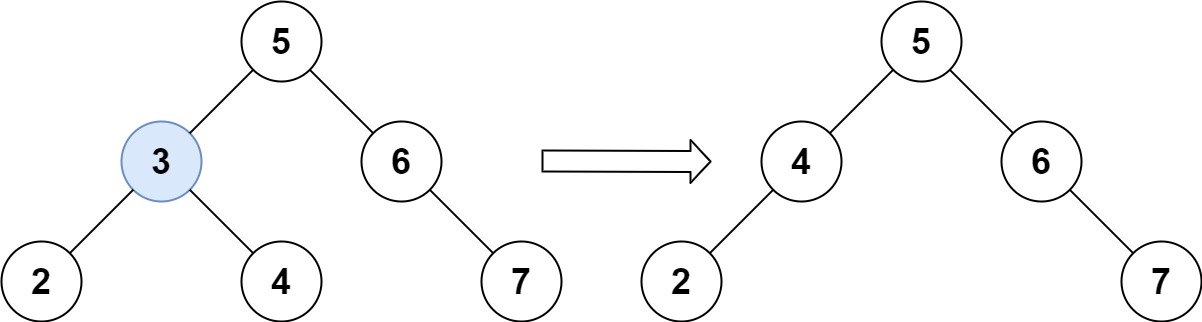
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.

Approach: Approach is going to be same as mentioned in the question itself. First we find the node using the approach in search in binary search tree. 

Now the removal part is lil tricky. Here are the steps we can take:

• If the node to remove is leaf node, we simply remove it.
• If the node has just one child then we can just assign node to it's child.
• Now the most tricky situation where both the children are not null, here we can take one of the following two appoaches:

1. Take the right most child of node's left subtree. Assign it's value to node's value. Now call this method recursively to remove this value from node's left subtree.
2. Take the left most child of node's right subtree. Assign it's value to node's value. Now call this method recursively to remove this value from node's right subtree.

That's all!

Implemenation in C#:

    public TreeNode DeleteNode(TreeNode root, int key)

    {

        if (root == null)

        {

            return root;

        }

        if (root.val == key)

        {

            if (root.right != null && root.left != null)

            {

                root.val = this.FindLeftMostNodeValue(root.right);

                root.right = this.DeleteNode(root.right, root.val);

            }

            else

            {

                if (root.left != null)

                {

                    return root.left;

                }

                else

                {

                    return root.right;

                }

            }

        }

        if (root.val < key)

        {

            root.right = this.DeleteNode(root.right, key);

        }

        else

        {

            root.left = this.DeleteNode(root.left, key);

        }      

        return root;

    }

    private int FindLeftMostNodeValue(TreeNode node)

    {

        while(node.left != null)

        {

            node = node.left;

        }

        return node.val;

    }

Complexity: O(n)