Problem: You are given an integer n. You have an n x n binary grid grid with all values initially 1's except for some indices given in the array mines. The ith element of the array mines is defined as mines[i] = [xi, yi] where grid[xi][yi] == 0.
Return the order of the largest axis-aligned plus sign of 1's contained in grid. If there is none, return 0.
An axis-aligned plus sign of 1's of order k has some center grid[r][c] == 1 along with four arms of length k - 1 going up, down, left, and right, and made of 1's. Note that there could be 0's or 1's beyond the arms of the plus sign, only the relevant area of the plus sign is checked for 1's.
Example:
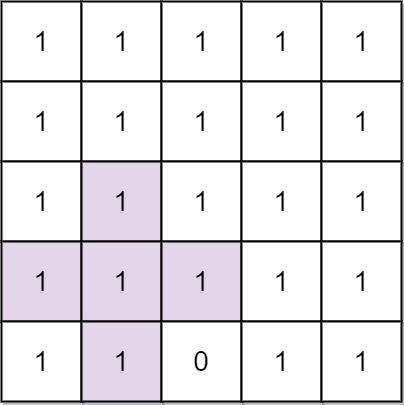
Input: n = 5, mines = [[4,2]]
Output: 2
Explanation: In the above grid, the largest plus sign can only be of order 2. One of them is shown.

Input: n = 1, mines = [[0,0]]
Output: 0
Explanation: There is no plus sign, so return 0.
Approach: The brute force approach would be to take every cell as center and calculate the length of biggest plus it can produce. The maximum of these lengths will be our answer but this will take O(n^3) time. Let's try to optimize it.
We can use DP here. Let's see at given cell (i, j) what could be the longest plus size:
Min(Size of contiguous 1's on the left, Size of contiguous 1's on the right, Size of contiguous 1's down side, Size of contiguous 1's up)
Now we just need to calculate the max of above for calculation for every cell. Now we need to see how we can calculate the left/right/up/down contiguous 1s efficiently. We can use DP here to calculate it in O(n^2). We can maintain 4 tables each for left, right, up and down and we can fill it in following way:
- Left[i][j] = if matrix[i][j] == 0 then 0 else Left[i][j-1] + 1
- Right[i][j] = if matrix[i][j] == 0 then 0 else Right[i][j+1] + 1
- Down[i][j] = if matrix[i][j] == 0 then 0 else Down[i-1][j] + 1
- Up[i][j] = if matrix[i][j] == 0 then 0 else Up[i+1][j] + 1
Now once we calculate it we can go at every cell (i, j) calculate the min of Left[i][j], Right[i][j], Down[i][j] and Up[i][j] say minVal[i][j]. In the end we can return max of all the minVal[i][j]s.
The above approach will solve the problem in O(n^2) and will work well but as you can see we are taking four 2D tables. We can apply the same algorithm using one 2D table only. The steps remains almost same and you can understand it by just looking at the implementation of our approach 2.
Implementation in C#:
Approach 1: Using four tables:
public int OrderOfLargestPlusSign(int n, int[][] mines)
{
HashSet<int> minesSet = new HashSet<int>();
foreach (int[] mine in mines)
{
minesSet.Add(mine[0] * n + mine[1]);
}
int[,] leftTable = new int[n,n];
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < n; ++j)
{
if (j == 0)
{
leftTable[i, j] = minesSet.Contains(i * n + j) ? 0 : 1;
}
else
{
leftTable[i, j] = minesSet.Contains(i * n + j) ? 0 : leftTable[i, j - 1] + 1;
}
}
}
int[,] rightTable = new int[n,n];
for (int i = 0; i < n; ++i)
{
for (int j = n - 1; j >= 0; --j)
{
if (j == n - 1)
{
rightTable[i, j] = minesSet.Contains(i * n + j) ? 0 : 1;
}
else
{
rightTable[i, j] = minesSet.Contains(i * n + j) ? 0 : rightTable[i, j + 1] + 1;
}
}
}
int[,] downTable = new int[n,n];
for (int j = 0; j < n; ++j)
{
for (int i = 0; i < n; ++i)
{
if (i == 0)
{
downTable[i, j] = minesSet.Contains(i * n + j) ? 0 : 1;
}
else
{
downTable[i, j] = minesSet.Contains(i * n + j) ? 0 : downTable[i - 1, j] + 1;
}
}
}
int[,] upTable = new int[n,n];
for (int j = 0; j < n; ++j)
{
for (int i = n - 1; i >= 0; --i)
{
if (i == n - 1)
{
upTable[i, j] = minesSet.Contains(i * n + j) ? 0 : 1;
}
else
{
upTable[i, j] = minesSet.Contains(i * n + j) ? 0 : upTable[i + 1, j] + 1;
}
}
}
int maxLength = 0;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < n; ++j)
{
int currLength = this.MinElement(leftTable[i, j], rightTable[i, j], downTable[i, j], upTable[i, j]);
maxLength = Math.Max(maxLength, currLength);
}
}
return maxLength;
}
private int MinElement(params int[] nums)
{
return nums.Min();
}
Approach 2: Using only one table:
public int OrderOfLargestPlusSign(int n, int[][] mines)
{
HashSet<int> minesSet = new HashSet<int>();
foreach (int[] mine in mines)
{
// We can use it as matrix size is nxn
minesSet.Add(mine[0] * n + mine[1]);
}
int[,] table = new int[n,n];
int maxLength = 0, count;
for (int i = 0; i < n; ++i)
{
count = 0;
// left
for (int j = 0; j < n; ++j)
{
count = minesSet.Contains(i * n + j) ? 0 : count + 1;
table[i,j] = count;
}
// right
count = 0;
for (int j = n - 1; j >= 0; --j)
{
count = minesSet.Contains(i * n + j) ? 0 : count + 1;
table[i, j] = Math.Min(table[i, j], count);
}
}
for (int j = 0; j < n; ++j)
{
// down
count = 0;
for (int i = 0; i < n; ++i)
{
count = minesSet.Contains(i * n + j) ? 0 : count + 1;
table[i, j] = Math.Min(table[i, j], count);
}
//up
count = 0;
for (int i = n - 1; i >= 0; --i)
{
count = minesSet.Contains(i * n + j) ? 0 : count + 1;
table[i, j] = Math.Min(table[i, j], count);
if (table[i, j] > maxLength)
{
maxLength = table[i, j];
}
}
}
return maxLength;
}
Complexity: O(n^2)