Problem: Given an m x n board of characters and a list of strings words, return all words on the board.
Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
Example:

Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]
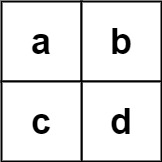
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []
Approach: The problem is similar to the problem of search a word in a matrix except here we are given an array of words. We will have the similar backtracking approach here too but we will use Trie to make it more efficient.
Implementation:
public class TrieNode
{
public const short ALPHABET_SIZE = 26;
public TrieNode(char value)
{
this.Value = value;
this.Children = new TrieNode[ALPHABET_SIZE];
this.End = 0;
}
public char Value { get; set; }
public TrieNode[] Children { get; set; }
public string Word { get; set; }
public int End { get; set; }
}
public class Trie
{
public Trie()
{
this.root = new TrieNode('/'); // special charater for root
}
public void Insert(string word)
{
TrieNode node = root;
foreach(char ch in word)
{
if (node.Children[ch - 'a'] == null)
{
node.Children[ch - 'a'] = new TrieNode(ch);
}
node = node.Children[ch - 'a'];
}
node.End++;
node.Word = word;
}
public void SearchOnBoard(char[][] board, int i, int j, List<string> result)
{
if (this.root.Children[board[i][j] - 'a'] == null)
{
return;
}
this.SearchOnBoard(this.root, board, i, j, result);
}
private void SearchOnBoard(TrieNode node, char[][] board, int i, int j, List<string> result)
{
int index = board[i][j] - 'a';
if (board[i][j] == '#' || node.Children[index] == null)
{
return;
}
node = node.Children[index];
if (node.End > 0)
{
result.Add(node.Word);
node.End--;
}
char temp = board[i][j];
board[i][j] = '#'; // visited
if (i > 0)
{
SearchOnBoard(node, board, i - 1, j, result);
}
if (i < board.Length - 1)
{
SearchOnBoard(node, board, i + 1, j, result);
}
if (j > 0)
{
SearchOnBoard(node, board, i, j - 1, result);
}
if (j < board[0].Length - 1)
{
SearchOnBoard(node, board, i, j + 1, result);
}
board[i][j] = temp;
}
private TrieNode root;
}
public class Solution
{
public IList<string> FindWords(char[][] board, string[] words)
{
List<string> result = new List<string>();
int rows = board?.Length ?? 0;
if (rows == 0)
{
return result;
}
int cols = board[0].Length;
int length = words.Length;
if (length == 0)
{
return result;
}
Trie trie = new Trie();
foreach(string word in words)
{
trie.Insert(word);
}
for (int i = 0; i < rows; ++i)
{
for (int j = 0; j < cols; ++j)
{
trie.SearchOnBoard(board, i, j, result);
}
}
return result;
}
}
Complexity: O( rows * cols * 3 ^ (length of the largest word in words))





