[LeetCode] Island Perimeter

Problem: You are given row x col grid representing a map where grid[i][j] = 1 represents land and grid[i][j] = 0 represents water.

Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).

The island doesn't have "lakes", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.

Example:

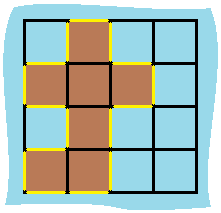
Input: grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
Output: 16
Explanation: The perimeter is the 16 yellow stripes in the image above.

Input: grid = [[1]]
Output: 4

Input: grid = [[1,0]]
Output: 4

Constraints:

• row == grid.length
• col == grid[i].length
• 1 <= row, col <= 100
• grid[i][j] is 0 or 1.
• There is exactly one island in grid.

Approach: If a cell is land then its contribution to island's perimeter is 4 initially. In case of any land neighbour cell of current cell means from the current cell one side is gone which was part of perimeter of the island so we need to subtract 1 from the perimeter. With this intuition we can have following approach:

• FOR i = 0 to rows
• FOR j = 0 to cols
• IF grid[i][j] == 1
• perimeter = perimeter + 4
• IF left cell is 1 
• perimenter = perimeter - 1
• IF right cell is 1 
• perimenter = perimeter - 1
• IF up cell is 1 
• perimenter = perimeter - 1
• IF down cell is 1 
• perimenter = perimeter - 1

Implementation in C#:

    public int IslandPerimeter(int[][] grid) 

    {

        int rows = grid?.Length ?? 0;

        if (rows == 0)

        {

            return 0;

        }

        int cols = grid[0].Length;

        int perimeter = 0;

        for (int i = 0; i < rows; ++i)

        {

            for (int j = 0; j < cols; ++j)

            {

                if (grid[i][j] == 1)

                {

                    perimeter += 4;

                    // Left neighbour

                    if (j - 1 >= 0 && grid[i][j -1] == 1)

                    {

                        --perimeter;

                    }

                    // Right neighbour

                    if (j + 1 < cols && grid[i][j + 1] == 1)

                    {

                        --perimeter;

                    }

                    // Up neighbour

                    if (i - 1 >= 0 && grid[i - 1][j] == 1)

                    {

                        --perimeter;

                    }

                    // Down neighbour

                    if (i + 1 < rows && grid[i + 1][j] == 1)

                    {

                        --perimeter;

                    }

                }

            }

        }

        return perimeter;

    }

Complexity: O(m * n) where m is number of rows and n is number of columns.