[LeetCode] 01 Matrix

Problem: Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Example:

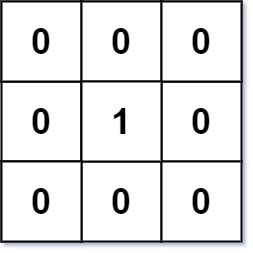
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

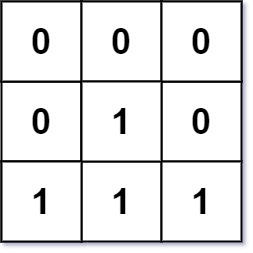
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• There is at least one 0 in mat.

Approach: This problem is getting the minimum distance between nodes of a graph. A node (cell) is connected to other node (cell) in case they are neighbours (left, right, up, down). Now we just need to calculate the minimum distance of cells with 0 to cells with 1. 

Given we need to calculate minimum distance, we need to apply the BFS here. That's all!

Implementation in C#:

    public int[][] UpdateMatrix(int[][] mat) 

    {

        int rows = mat?.Length ?? 0;

        if (rows == 0)

        {

            return new int[][]{};     

        }

        int cols = mat[0].Length;

        bool[,] visited = new bool[rows, cols];        

        Queue<int[]> queue = new Queue<int[]>();

        this.AddZeroCellsToQueue(mat, queue, visited);

        while (queue.Count != 0)

        {

            int[] cell = queue.Dequeue();

            this.UpdateNeighboursAndAddToQueueIfValid(mat, queue, visited, cell[0], cell[1]);

        }

        return mat;

    }

    

    private void UpdateNeighboursAndAddToQueueIfValid(

        int[][] mat, 

        Queue<int[]> queue, 

        bool[,] visited,

        int row,

        int col

    )

    {

        // up

        this.UpdateCellAndAddToQueueIfValid(mat, queue, visited, row, col, row - 1, col);

        // down

        this.UpdateCellAndAddToQueueIfValid(mat, queue, visited, row, col, row + 1, col);

        // left

        this.UpdateCellAndAddToQueueIfValid(mat, queue, visited, row, col, row, col - 1);

        // right

        this.UpdateCellAndAddToQueueIfValid(mat, queue, visited, row, col, row, col + 1);

    }

    

    private void UpdateCellAndAddToQueueIfValid(

        int[][] mat, 

        Queue<int[]> queue, 

        bool[,] visited,

        int parentRow,

        int parentCol,

        int row,

        int col

    )

    {

        if ( row < 0 

            || row >= mat.Length

            || col < 0

            || col >= mat[0].Length

            || visited[row, col]

           )

        {

            return;

        }        

        mat[row][col] = mat[parentRow][parentCol] + 1;

        visited[row, col] = true;

        queue.Enqueue(new int[] { row, col });

    }

    

    private void AddZeroCellsToQueue(int[][] mat, Queue<int[]> queue, bool[,] visited)

    {

        for (int i = 0; i < mat.Length; ++i)

        {

            for (int j = 0; j < mat[0].Length; ++j)

            {

                if (mat[i][j] == 0)

                {

                    queue.Enqueue(new int[] {i, j});

                    visited[i, j] = true;

                }

            }

        }

    }

Complexity: O(m * n)

[LeetCode] Beautiful Array

Problem: For some fixed n, an array nums is beautiful if it is a permutation of the integers 1, 2, ..., n, such that:

For every i < j, there is no k with i < k < j such that nums[k] * 2 = nums[i] + nums[j].

Given n, return any beautiful array nums.  (It is guaranteed that one exists.)

Example:

Input: n = 4
Output: [2,1,4,3]

Input: n = 5
Output: [3,1,2,5,4]

Approach: Let's try to understand the condition:

i < k < j such that nums[k] * 2 = nums[i] + nums[j]

what it is saying that for every 1 <= k <= n - 2, there are no element in left of k and right of k such that the sum of those elements is equal to 2 * k. How we can ensure it? if we see closely:

2 * nums[k] is even for any nums[k].

so if we keep odd numbers to the left of k and even numbers to the right of k. We will be able to achieve it as sum of an even number and an odd number can't be even. We can achieve it by using divide and conquer approach; basically we first divide the array in two halves and then create the beautiful array of each half recursively and then concatenate theses two arrays(halves).

Let's see how we can do it? The shortest beautiful array is [1,3,2] or [3,1,2]. Right, how to get this array:

Here n is 3 so what we can do we can divid this into two halves:

• Number of odd numbers = (n + 1) / 2 = (3 + 1) / 2 = 2 so the first half is [1,2] for now.
• Number of even numbers = n / 2 = 3 / 2 = 1 so the second half is [1] for now.

There are some problems with these halves right, as both halves have 1 in it. Odd half has 2 and even half has 1. Let's see how to actually generate right halves:

• The odd numbers will be 2 * oddHalf[i] - 1 so the first half will become [2 * 1 - 1, 2 * 2 - 1] = [1,3]
• The even numbers will be 2 * evenHalf[i] so the second half will become [2 * 1] = [2]

Now we have generated these halves we can just concatenate these halves and it will become [1,3,2] which is our answer. Now that the approach is clear, here is how our algorithm looks like:

• DEF Solve(n):
• IF n == 1:
• RETURN [1]
• oddHalf = Solve((n + 1) / 2)
• evenHalf = Solve(n/2)
• result = []
• int writeIndex = 0
• FOR i = 0 TO length of oddHalf
• result[writeIndex] = 2 * oddHalf[i] - 1
• writeIndex = writeIndex + 1
• FOR i = 0 TO length of evenHalf
• result[writeIndex] = 2 * evenHalf[i]
• writeIndex = writeIndex + 1
• RETURN result

In the implementation I have just taken a hashmap and store the intermediate results in it so that we don't have to recalculate the result for same intermediate n and in that way we can save some time.

Implementation in C#:

    public int[] BeautifulArray(int n) 

    {

        Dictionary<int, int[]> resultDict = new Dictionary<int, int[]>();

        return this.SolveBeautifulArray(n, resultDict);

    }

    

    private int[] SolveBeautifulArray(int n, Dictionary<int, int[]> resultDict)

    {

        if (resultDict.ContainsKey(n))

        {

            return resultDict[n];

        }        

        int[] result = new int[n];

        if (n == 1)

        {

            result[0] = 1;

            resultDict.Add(1, result);

            return result;

        }

        int i = 0;

        // odd nums

        foreach (int x in this.SolveBeautifulArray((n + 1) / 2, resultDict))

        {

            result[i++] = 2 * x - 1;

        }

        // even nums

        foreach (int x in this.SolveBeautifulArray(n / 2, resultDict))

        {

            result[i++] = 2 * x;

        }

        resultDict.Add(n, result);        

        return result;

    }

Complexity: O(nlogn)

[LeetCode] Swap Nodes in Pairs

Problem: Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list's nodes (i.e., only nodes themselves may be changed.)

Example:

Input: head = [1,2,3,4]
Output: [2,1,4,3]

Input: head = []
Output: []

Input: head = [1]
Output: [1]

Approach: Not much to explain as it is very much a straight forward problem to solve. You can understand the approach by just looking at the implementation.

Implementation in C#:

        public ListNode SwapPairs(ListNode head)

    {

if (head?.next == null)

{

return head;

}

ListNode node1 = head;

ListNode node2 = head.next;

head = head.next;

ListNode prev = null;

while(node1 != null && node2 != null)

{

ListNode next = node2.next;

node2.next = node1;

node1.next = next;

if (prev != null)

{

prev.next = node2;

}

prev = node1;

node1 = next;

node2 = node1?.next;

}

return head;

}

Complexity: O(n)

[LeetCode] Binary Tree Pruning

Problem: Given the root of a binary tree, return the same tree where every subtree (of the given tree) not containing a 1 has been removed.

A subtree of a node node is node plus every node that is a descendant of node.

Example:

Input: root = [1,null,0,0,1]
Output: [1,null,0,null,1]
Explanation: 
Only the red nodes satisfy the property "every subtree not containing a 1".
The diagram on the right represents the answer.

Input: root = [1,0,1,0,0,0,1]
Output: [1,null,1,null,1]

Input: root = [1,1,0,1,1,0,1,0]
Output: [1,1,0,1,1,null,1]

Approach: We can simply do a post order traversal here to solve this problem. Just look at the implementation to understand the approach.

Implementation in C#:

    public TreeNode PruneTree(TreeNode root) 

    {

        if (root == null)

        {

            return null;

        }        

        root.left = this.PruneTree(root.left);

        root.right = this.PruneTree(root.right);

        return root.left == null && root.right == null && root.val == 0 ? null : root;

    }

Complexity: O(n)

[LeetCode] Partition Array into Disjoint Intervals

Problem: Given an array nums, partition it into two (contiguous) subarrays left and right so that:

• Every element in left is less than or equal to every element in right.
• left and right are non-empty.
• left has the smallest possible size.

Return the length of left after such a partitioning.  It is guaranteed that such a partitioning exists.

Example:

Input: nums = [5,0,3,8,6]
Output: 3
Explanation: left = [5,0,3], right = [8,6]

Input: nums = [1,1,1,0,6,12]
Output: 4
Explanation: left = [1,1,1,0], right = [6,12]

Approach: A straight forward approach would be to check for every index 'i' where all nums[0]...nums[i-1]  are less than or equal to nums[i]...nums[n-1] where n is number of elements in the array nums but it will be an expensive solution.

If you look closely what we are trying to do here is to check 

Max(nums[0]...nums[i-1]) <= Min(nums[i]...nums[n-1]

Right! With keeping this mind we can maintain two arrays say maxLeft and minRight where maxLeft[i] is the Max(nums[0]...nums[i]) and minRight[i] is Min(nums[i]...nums[n-1]). We can easily generate these arrays in linear time.

Once the above arrays are generated we can just check if maxLeft[i-1] <= minRight[i] is true or false. If true then we can return i. 

If the above approach is clear then there is one minor optimisation we can do in terms of space. We can use a int variable instead of maintaining the maxLeft array. You can look at implementation to understand this approach. 

Implementation in C#:

    public int PartitionDisjoint(int[] nums) 

    {

        int length = nums?.Length ?? 0;

        if (length <= 1)

        {

            return length;

        }

        int[] minRight = new int[length];

        minRight[length - 1] = nums[length - 1];

        for (int i = length - 2; i >= 0; --i)

        {

            minRight[i] = Math.Min(minRight[i + 1], nums[i]);

        }

        int maxLeft = nums[0];

        for (int i = 0; i < length - 1; ++i)

        {

            maxLeft = Math.Max(maxLeft, nums[i]);

            if (maxLeft <= minRight[i + 1])

            {

                return i + 1;

            }

        }        

        return -1;

    }

Complexity: O(n)

[LeetCode] Rotate Image

Problem: You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example:

Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]

Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

Input: matrix = [[1]]
Output: [[1]]

Input: matrix = [[1,2],[3,4]]
Output: [[3,1],[4,2]]

Approach: The approach is straight forward:

• Transpose the matrix.
• Reverse each row. 

Implementation in C#:

    public void Rotate(int[][] matrix)

    {

        int n = matrix?.Length ?? 0;

        if (n == 0)

        {

            return;

        }

        for (int i = 0; i < n; ++i)

        {

            for (int j = 0; j <= i; ++j)

            {

                int temp = matrix[i][j];

                matrix[i][j] = matrix[j][i];

                matrix[j][i] = temp;

            }

        }

        for (int i = 0; i < n; ++i)

        {

            Array.Reverse(matrix[i]);

        }

    }

Complexity: O(n^2)

[LeetCode] Custom Sort String

Problem: order and str are strings composed of lowercase letters. In order, no letter occurs more than once.

order was sorted in some custom order previously. We want to permute the characters of str so that they match the order that order was sorted. More specifically, if x occurs before y in order, then x should occur before y in the returned string.

Return any permutation of str (as a string) that satisfies this property.

Example:

Input: 
order = "cba"
str = "abcd"
Output: "cbad"
Explanation: 
"a", "b", "c" appear in order, so the order of "a", "b", "c" should be "c", "b", and "a". Since "d" does not appear in order, it can be at any position in the returned string. "dcba", "cdba", "cbda" are also valid outputs.

Approach: We can just use the custom comparator while sorting the input string "str" using the indices of "order". It's a straight forward problem to solve which can be understood by just looking at the code.

Implementation in C#:

    public string CustomSortString(string order, string str) 

    {

        int [] orderArr = new int[26];

        for (int i = 0; i < order.Length; ++i)

        {

            orderArr[order[i] - 'a'] = i;

        }    

        char[] strArr = str.ToCharArray();

        Array.Sort(strArr, (x, y) => {

            return orderArr[x - 'a'].CompareTo( orderArr[y - 'a']);

        });

        return new string(strArr);

    }

Complexity: O ( m + nlogn) where m is length of order and n is length of str.

[Uber][LeetCode] Generate Parentheses

Problem: Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.  

Example:

Input: n = 3
Output: ["((()))","(()())","(())()","()(())","()()()"]

Input: n = 1
Output: ["()"]

Approach: The first direct approach would be generate all the 2^2n combinations and add the valid combinations to the result. We can easily generate all the valid combinations using backtracking.

We can make the above approach a little better, instead of adding '(' and ')' blindly, we can add them when we know it will remain a valid sequence. We can maintain count of open and close braces to achieve it. We know that we can have at max 'n' open and close braces so we add '(' if its count is less than or equal to 'n' and we add ')' only if its count is less than or equal to count of open braces.

That's all!

Implementation in C#:

Approach 1:

   public IList<string> GenerateParenthesis(int n) 

   {

        List<string> result = new List<string>();

        char[] curr = new char[2 * n];

        this.GenerateParenthesis(curr, 0, result);

        return result;

    }

    private void GenerateParenthesis(char[] curr, int currPos, List<string> result)

    {

        if (currPos == curr.Length)

        {

            if (this.IsValid(curr))

            {

                result.Add(new string(curr));

            }

            return;

        }

        curr[currPos] = '(';

        this.GenerateParenthesis(curr, currPos + 1, result);

        curr[currPos] = ')';

        this.GenerateParenthesis(curr, currPos + 1, result);

    }

    

    private bool IsValid(char[] curr)

    {

        int count = 0;

        foreach(char ch in curr)

        {

            if (ch == '(')

            {

                ++count;

            }

            else

            {

                --count;

            }            

            if (count < 0)

            {

                return false;

            }

        }  

        return count == 0;

    }

Approach 2:

    public IList<string> GenerateParenthesis(int n) 

    {

        List<string> result = new List<string>();

        char[] curr = new char[2 * n];

        this.GenerateParenthesis(curr, 0, result, n, 0, 0);

        return result;

    }

    

    private void GenerateParenthesis(char[] curr, int currPos, List<string> result, int limit, int open, int close)

    {

        if (currPos == curr.Length)

        {

            result.Add(new string(curr));

            return;

        }

        if (open < limit)

        {

            curr[currPos] = '(';

            this.GenerateParenthesis(curr, currPos + 1, result, limit, open + 1, close);

        }

        if(close < open)

        {

            curr[currPos] = ')';

            this.GenerateParenthesis(curr, currPos + 1, result, limit, open, close + 1);

        }

    }

Complexity: Approach 1: O(2^2n * n) Validation of 2^2n combinations of length n

                     Approach 2: O( 4^n / sqrt(n)) nth catalan number * n = (4 ^ n / (n * sqrt(n)) * n