Problem: Given an m x n matrix grid where each cell is either a wall 'W', an enemy 'E' or empty '0', return the maximum enemies you can kill using one bomb. You can only place the bomb in an empty cell.
The bomb kills all the enemies in the same row and column from the planted point until it hits the wall since it is too strong to be destroyed.
Example:
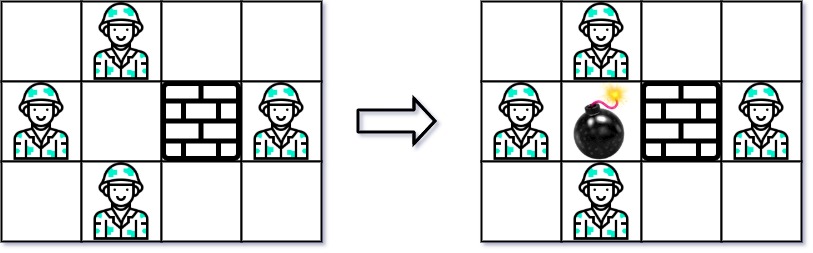
Input: grid = [["0","E","0","0"],["E","0","W","E"],["0","E","0","0"]] Output: 3
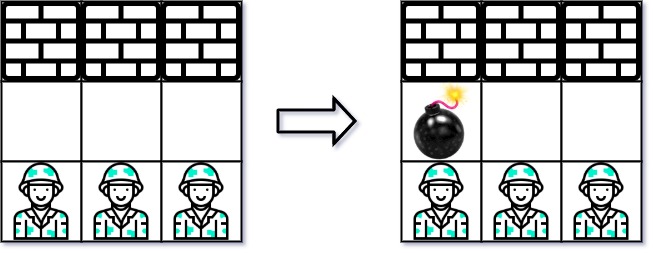
Input: grid = [["W","W","W"],["0","0","0"],["E","E","E"]] Output: 1
Constraints:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 500
- grid[i][j] is either 'W', 'E', or '0'.
Approach: The immediate approach which comes to mind is to place bomb at every cell and count the number of enemies which we can kill. We just take the maximum of these counts. Have a look at implementation to understand the approach in detail.
The above approach will solve the problem but it is expensive as it will take O (m * n * (m + n)) ~= O(n^3) time. Let's try to improve it.
If you see in the above approach, we are solving same subproblem multiple times. Let's look at the following row:
['0', '0', 'E', '0']
If you see the number of enemies killed in this row will always be 1 regardless the cell where we can place the bomb. If we see the problem closely we can find a pattern that then number of enemies killed in a row will be changed only if it is the first cell of the row (0th column) or the previous cell (curr_col - 1) is a wall.
That means we can have one variable say rowHits for every row which will be changed only in case of first cell or cell after the wall.
We can do the same for the columns also but with one change; we need to have colHits array instead of one variable like rowHits. Why? This is because we have loops like following:
- FOR row = 0 To m - 1
- For col = 0 TO n - 1
If you see the loops we are completing one row first and then going to second row so one variable is okay to have but in case of columns we need to go over all the columns for each row. That's why we need colHits as an array to keep track of all the colHits.
That's all! Look at the implementation for the details.
Implementation in C#:
Approach 1: Brute-force:
public int MaxKilledEnemies(char[][] grid)
{
int rows = grid.Length;
int cols = grid[0].Length;
int maxKilledEnemies = 0;
for (int i = 0; i < rows; ++i)
{
for (int j = 0; j < cols; ++j)
{
if (grid[i][j] == '0')
{
maxKilledEnemies = Math.Max(maxKilledEnemies, this.CountReachableEnemies(grid, i, j));
}
}
}
return maxKilledEnemies;
}
private int CountReachableEnemies(char[][] grid, int row, int col)
{
int rows = grid.Length;
int cols = grid[0].Length;
int totalEnemies = this.CountReachableEnemiesInRow(grid, row, col);
totalEnemies += this.CountReachableEnemiesInColumn(grid, row, col);
return totalEnemies;
}
private int CountReachableEnemiesInRow(char[][] grid, int row, int col)
{
int cols = grid[0].Length;
int totalEnemies = 0;
for (int i = col - 1; i >= 0; --i)
{
if (grid[row][i] == 'W')
{
break;
}
if (grid[row][i] == 'E')
{
++totalEnemies;
}
}
for (int i = col + 1; i < cols; ++i)
{
if (grid[row][i] == 'W')
{
break;
}
if (grid[row][i] == 'E')
{
++totalEnemies;
}
}
return totalEnemies;
}
private int CountReachableEnemiesInColumn(char[][] grid, int row, int col)
{
int rows = grid.Length;
int totalEnemies = 0;
for (int i = row - 1; i >= 0; --i)
{
if (grid[i][col] == 'W')
{
break;
}
if (grid[i][col] == 'E')
{
++totalEnemies;
}
}
for (int i = row + 1; i < rows; ++i)
{
if (grid[i][col] == 'W')
{
break;
}
if (grid[i][col] == 'E')
{
++totalEnemies;
}
}
return totalEnemies;
}
Approach 2: Dynamic Programming:
public int MaxKilledEnemies(char[][] grid)
{
int rows = grid.Length;
int cols = grid[0].Length;
int maxKilledEnemies = 0, rowHits = 0;
int[] colHits = new int[cols];
for (int i = 0; i < rows; ++i)
{
for (int j = 0; j < cols; ++j)
{
if (j == 0 || grid[i][j - 1] == 'W')
{
rowHits = 0;
for (int k = j; k < cols; ++k)
{
if (grid[i][k] == 'W')
{
break;
}
if (grid[i][k] == 'E')
{
++rowHits;
}
}
}
if (i == 0 || grid[i - 1][j] == 'W')
{
colHits[j] = 0;
for (int k = i; k < rows; ++k)
{
if (grid[k][j] == 'W')
{
break;
}
if (grid[k][j] == 'E')
{
++colHits[j];
}
}
}
if (grid[i][j] == '0')
{
maxKilledEnemies = Math.Max(maxKilledEnemies, rowHits + colHits[j]);
}
}
}
return maxKilledEnemies;
}
Complexity: Approach 1: O(m * n * ( m + n), Approach 2: O(3 * m * n) = O(m * n)
No comments:
Post a Comment