K-th Smallest in Lexicographical Order

Problem: Given integers n and k, find the lexicographically k-th smallest integer in the range from 1 to n.

Example:

Input:
n: 14   k: 8

Output:
3

Explanation:
The lexicographical order is [1, 10, 11, 12, 13, 14, 2, 3, 4, 5, 6, 7, 8, 9], so the 8th smallest number is 3.

Approach: First approach which directly come to mind is create an array of size n, insert numbers 1...n,  sort the array in lexicographical Order and just return element at the (k - 1)th index. This will surely work but it will be expensive in terms of time. It will take at least nlogn time given string comparison is taking constant time.

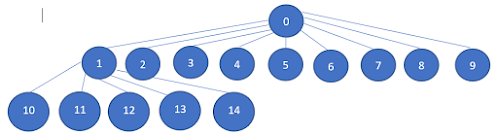
Let's think about this problem differently. If you look closely this is kind of forming a tree which each node is having <= 10 children. For our example, the tree will look like following:

Once we understood its structure, we can see we can apply DFS to to solve this question. That's all!

Implementation in C#:

        public static int FindKthNumber(int n, int k)

        {

            return (int)FindKthNumberDFS(1, n, k);

        }

        private static long FindKthNumberDFS(long start, long end, long k)

        {

            if (k == 1)

            {

                return start;

            }

            long childrenCount = GetNumberOfChildren(start, end);

            return childrenCount < k ? FindKthNumberDFS(start + 1, end, k - childrenCount) : FindKthNumberDFS(start * 10, end, k - 1);

        }

        private static long GetNumberOfChildren(long start, long end)

        {

            long rightSibling = start + 1;

            long childrenCount = 0;

            while(start <= end)

            {

                childrenCount += Math.Min(end + 1, rightSibling) - start;

                start *= 10;

                rightSibling *= 10;

            }

            return childrenCount;

        }

Complexity: O(logn)