[LeetCode] Number of Nodes in the Sub-Tree With the Same Label

Problem: You are given a tree (i.e. a connected, undirected graph that has no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges. The root of the tree is the node 0, and each node of the tree has a label which is a lower-case character given in the string labels (i.e. The node with the number i has the label labels[i]).

The edges array is given on the form edges[i] = [ai, bi], which means there is an edge between nodes ai and bi in the tree.

Return an array of size n where ans[i] is the number of nodes in the subtree of the ith node which have the same label as node i.

A subtree of a tree T is the tree consisting of a node in T and all of its descendant nodes.

Example:

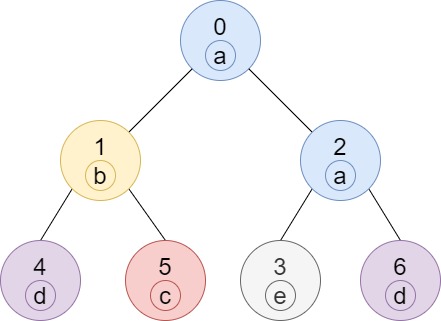
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
Output: [2,1,1,1,1,1,1]
Explanation: Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).

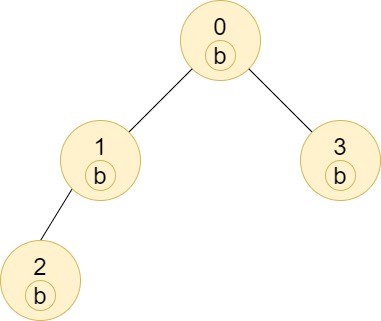
Input: n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
Output: [4,2,1,1]
Explanation: The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.

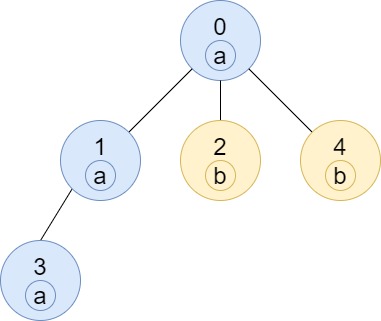
Input: n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
Output: [3,2,1,1,1]

Constraints:

• 1 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• labels.length == n
• labels is consisting of only of lowercase English letters.

Approach: We can use PostOrder traversal here as it visits the whole subtree before visiting the root of the subtree. Given it's an undirected graph, we just need to take care that we don't visit the same node more than once so we can use a visit set to avoid it.

Implementation in C#:

    public int[] CountSubTrees(int n, int[][] edges, string labels)

    {

        if (n == 0)

        {

            return new int[] {};

        }

        int length = edges?.Length ?? 0;

        int[] result = new int[n];

        if (length == 0)

        {

            return result;

        }

        var tree = this.MakeTree(edges);

        bool[] visited = new bool[n];

        this.CountSubTreesPostOrder(0, tree, visited, labels, result);

        return result;

    }

    private int[] CountSubTreesPostOrder(

                    int node,

                    Dictionary<int, List<int>> tree,

                    bool[] visited,

                    string labels,

                    int[] result)

    {

        int[] labelCountMap = new int[26];

        visited[node] = true;

        if (tree.ContainsKey(node))

        {

            foreach (int child in tree[node])

            {

                if (!visited[child])

                {

                    int[] childLabelCountMap = this.CountSubTreesPostOrder(

                                                child,

                                                tree,

                                                visited,

                                                labels,

                                                result);

                    for (int i = 0; i < 26; ++i)

                    {

                        labelCountMap[i] += childLabelCountMap[i];

                    }

                }

            }

        }

        result[node] = ++labelCountMap[labels[node] - 'a'];

        return labelCountMap;

    }

    private Dictionary<int, List<int>> MakeTree(int[][] edges)

    {

        var nodesMap = new Dictionary<int, List<int>>();

        foreach(int[] edge in edges)

        {

            if (!nodesMap.ContainsKey(edge[0]))

            {

                nodesMap[edge[0]] = new List<int>();

            }

            if (!nodesMap.ContainsKey(edge[1]))

            {

                nodesMap[edge[1]] = new List<int>();

            }

            nodesMap[edge[0]].Add(edge[1]);

            nodesMap[edge[1]].Add(edge[0]);

        }

        return nodesMap;

    }

Complexity: O(n)